fig4

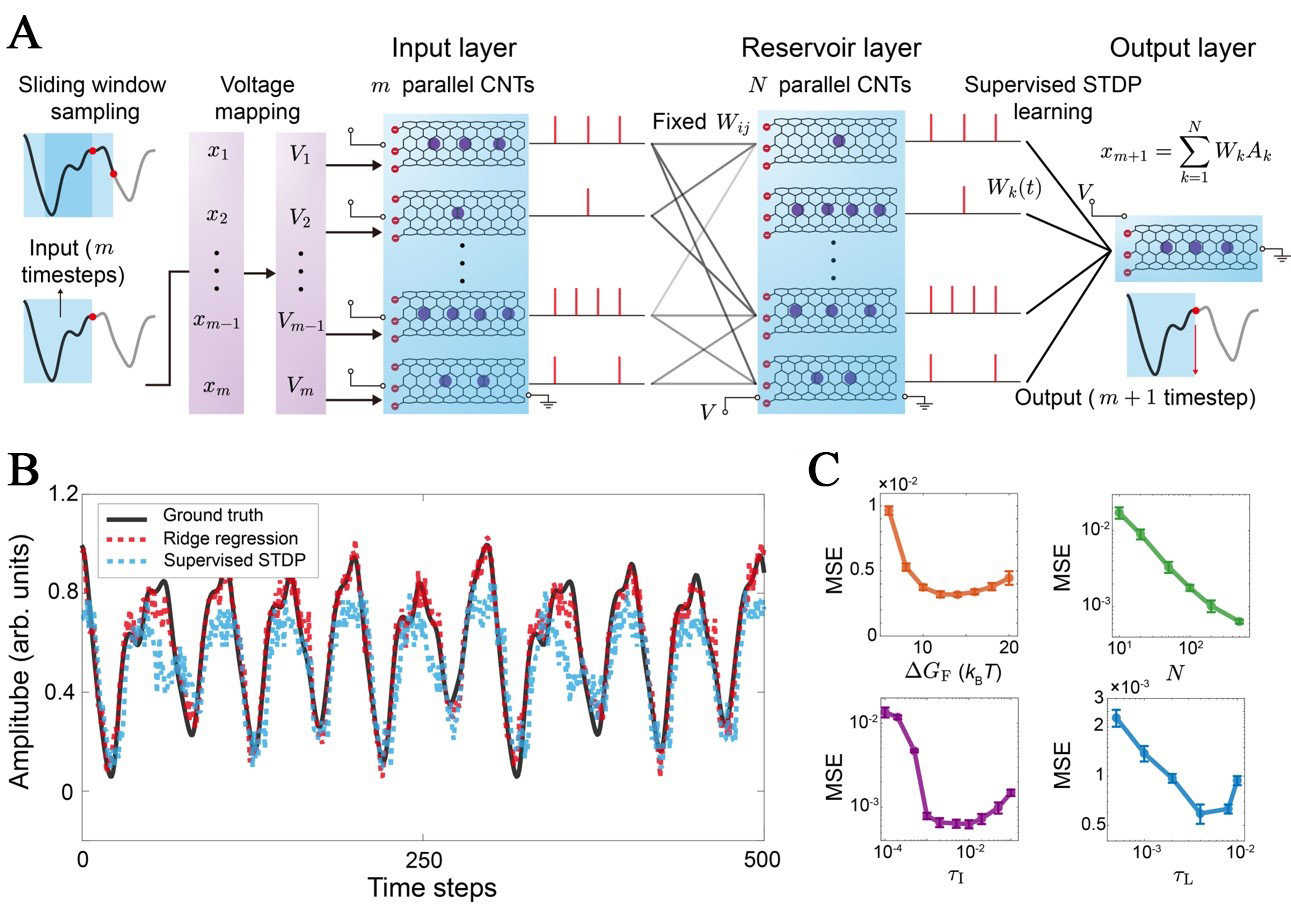
Figure 4. CNT-based reservoir computing architecture and performance analysis of (A) The overall architecture comprises three layers, including the Input Layer (M parallel CNTs), the Reservoir Layer (N parallel CNTs), and the Output Layer (single CNT). The input layer employs a sliding window sampling strategy to map m historical time-steps (x₁, …, x_M) onto corresponding analog voltages (V₁, …, V_M). These voltages drive the CNT encoders to generate stochastic ionbit streams [S_in(t)]. The reservoir layer uses fixed, sparse weights (W_ij) to project S_in(t) into an N-dimensional state space. The output layer features plastic weights (W_j) which are updated during training via a supervised STDP rule. The final output is the prediction of the target value (x_M+1); (B) The time-series prediction performance for the Mackey-Glass task demonstrates that the physically supervised STDP method successfully tracks the complex periodic dynamics; (C) The MSE of prediction is analyzed and optimized with respect to key physical parameters, including the intrinsic barrier height (ΔG_F), reservoir size (N), and the characteristic time constants of integration (τ_I) and leakage (τ_L). CNT: Carbon nanotube; STDP: spike-timing-dependent plasticity; MSE: mean-square error.