fig3

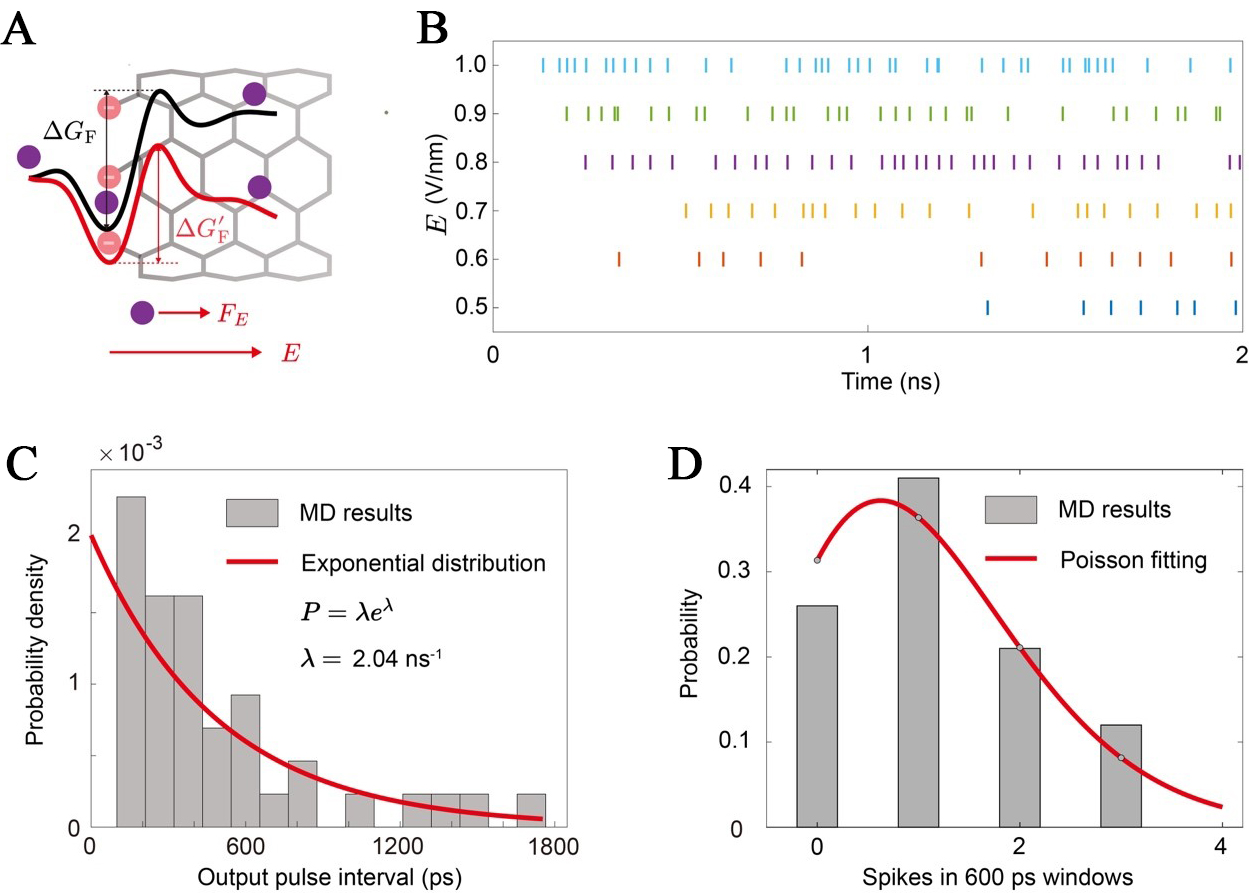
Figure 3. Stochastic firing dynamics of iontronic neurons. (A) Schematic of the ion transport energy landscape. Under no external field (top), an ion must overcome the intrinsic firing energy barrier (ΔG_F). An applied electric field, E, exerts a force (F_E) that effectively tilts the landscape, reducing the barrier to ΔG’_F (bottom), thereby increasing the probability of a firing event; (B) Spike raster plots showing output ionbits over a 2 ns window for different applied electric field strengths based on the MD results. As the field strength increases from 0.5 V/nm to 1.0 V/nm, the firing becomes more frequent and denser, demonstrating continuous rate modulation; (C) Probability density distribution of ISIs for electric fields of 0.5 V/nm. The distributions are well-fitted by exponential decay functions, a characteristic signature of a Poisson process; (D) Histogram of the number of spikes observed in 600 ps time windows for an applied field of 0.5 V/nm. The distribution of spike counts is accurately described by a Poisson fit (gray bars), further confirming the stochastic Poisson nature of the neuron’s output. MD: Molecular dynamics; ISI: inter-spike interval.