Effect of incision curvature on measuring fracture energy of soft materials

INTRODUCTION

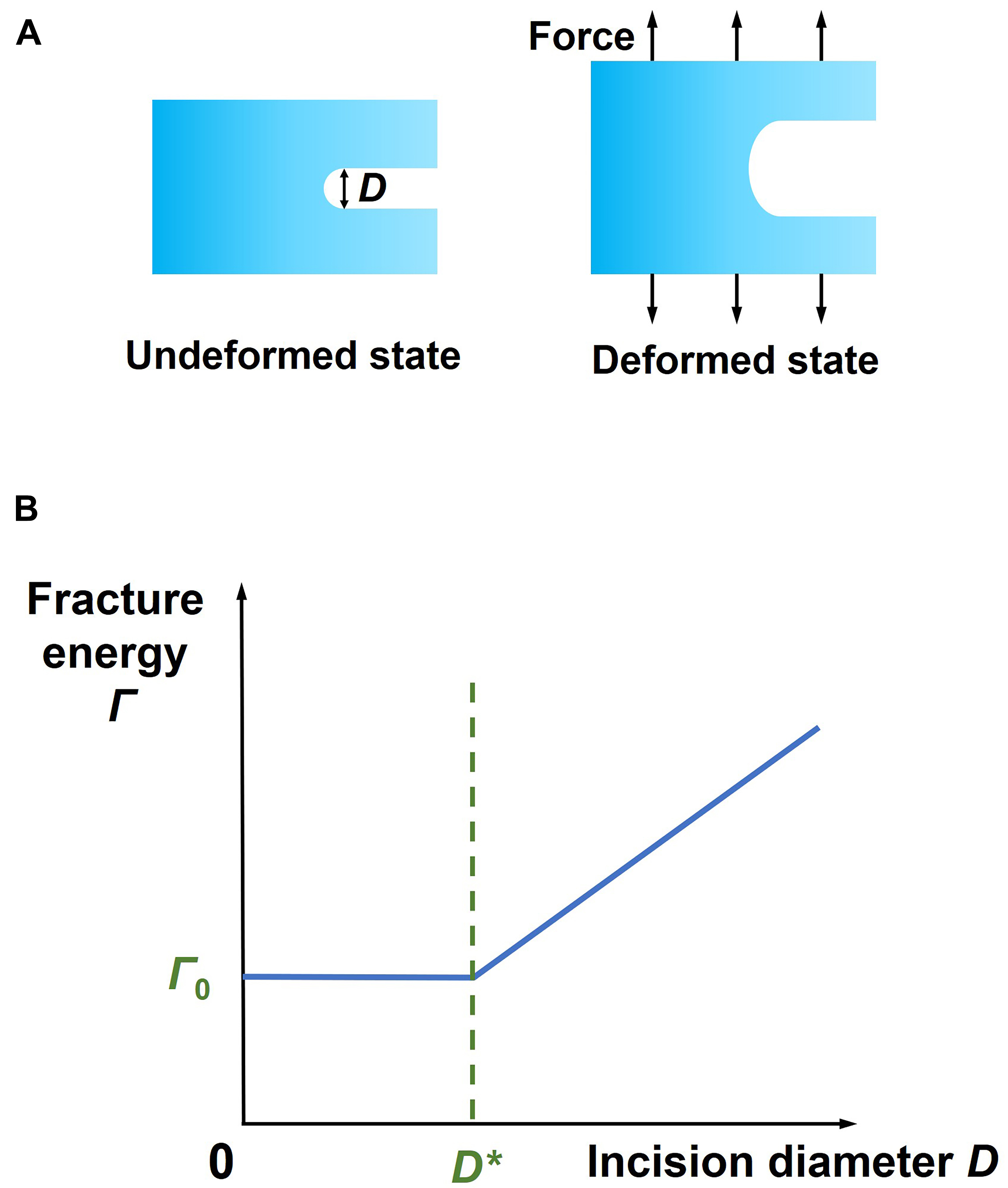
Work of fracture (unit: J/m³), sometimes called toughness in materials science, is defined by the area under the stress-strain curve, which is measured using a specimen without any pre-existing incision. Fracture energy (unit: J/m²), also called fracture toughness in mechanics, is defined as the energy needed to advance a crack per unit area, and is measured using a specimen with a pre-existing incision^[1-4]. These two mechanical properties are sometimes confused in literature. Fracture energy measures the resistance of a material to crack propagation. In measuring fracture energy, an incision must be introduced to the specimen while the incision always has a finite radius of curvature [Figure 1A], so that fracture energy is anticipated to depend on the incision curvature. Note that the incision curvature is defined in the undeformed state, and is irrelevant to the curvature of the blunting incision in the deformed state when subject to a load.

Figure 1. The effect of incision diameter on the fracture energy. (A) An elastic body contains an incision with a diameter D. Under an applied force, the incision opens and blunts; (B) The measured fracture energy Γ, depends on the incision diameter D. When D is smaller than a critical length D^*, Γ is a constant, independent of D. When D is larger than the critical length D^*, Γ increases with D.

The effect of incision curvature on fracture energy has been studied in many polymeric materials^[2,5,6]. In a pure shear test of a rubber, the measured fracture toughness is linearly proportional to the incision diameter within the 0.9-2.9 mm range^[5]. In a single edge notch bend test of an epoxy resin, the measured fracture energy remains constant when the incision diameter is below 0.2 μm, and is linearly proportional to the incision diameter within range of 0.2 μm to 3.5 mm^[6]. In a peeling test of a polyacrylamide hydrogel, the measured fracture toughness is positively correlated with the incision diameter^[2]. While these experimental results show the incision curvature-dependent fracture behavior, the underlying mechanism governing this phenomenon remains unresolved.

This effect is critical for establishing testing standards of fracture energy. For fracture energy testing of plastics (ASTM D5045-99; ASTM D6068-10), the incision is created by inserting a razor blade into a pre-notch, gently tapping it into the specimen, and promoting crack propagation ahead of the blade tip^[7-9]. For fracture energy testing of vulcanized rubber (ASTM D624-00), incisions are created using sharp blades without specified incision curvature^[10]. All polymer fracture energy measurement standards mandate sufficiently sharp incisions. However, current standards lack quantitative specifications for required incision sharpness.

In this study, we hypothesize that the fracture energy Γ and incision diameter D (inversely proportional to incision curvature) exhibit the relationship shown in Figure 1B. Below a transition length D^*, Γ remains constant (Γ₀) independent of D, whereas above D^*, Γ increases linearly with D. To test this hypothesis, polyacrylamide/Ca-alginate double-network hydrogels with fracture energy ~10³ J/m² were prepared. Fracture energy was measured as a function of incision diameter using pure shear configuration. The experimental results demonstrate strong agreement with the proposed hypothesis. The material exhibited a transition diameter of 0.48 ± 0.03 mm. The transition length scale correlates with the material's fractocohesive length, defined as fracture energy divided by work of fracture^[11]. Notably, the transition length scale differs from the inelasticity scale by three orders of magnitude in this material system.

The theoretical analysis can be understood as follows. Consider a semi-infinite incision in an infinite elastic body. When the incision is sufficiently sharp, upon rupture, the fracture process zone around incision tip reaches the work of fracture, W^*, and the measurement gives fracture energy, Γ₀. The size of fracture process zone can be roughly estimated by Γ₀/W^*[11]. The incision diameter D is the sole characteristic length in an infinite elastic body. When D is smaller than transition diameter D^*, the size of fracture process zone holds Γ₀/W^*, the measured fracture energy approaches Γ₀, which can be regarded as the intrinsic fracture energy independent of incision curvature. Above the transition length, the linear dependence of fracture energy on incision diameter was interpreted using a dimensional analysis. Consider the case where the incision diameter is larger, D > D^*. The existence of incision diameter alleviates the stress concentration at the incision tip. The stress at the incision tip is spread across a larger region. Upon rupture, a larger zone around the incision tip reaches the work of fracture, W^*. Since D is the sole characteristic length scale in the fracture process, fracture energy Γ and work of fracture W^* have the relation, Γ = W^*D. A similar argument was made by Thomas in 1955^[5]. In Thomas’s paper, he performed experiments and verified the hypothesis of the linear relationship. As the diameter D decreases, the fracture energy Γ decreases linearly, but cannot fall below the intrinsic fracture energy, Γ₀. Therefore, a transition diameter exists, D^* ~ Γ₀/W^*. This quantity, Γ₀/W^*, is defined in the literature as the fractocohesive length^[11].

In a testing specimen, the boundary of specimen introduces additional geometric lengths. Thus, the incision diameter is not the only characteristic length in the system. The measured fracture energy should depend on the geometry of specimen as well. To study the effect of incision diameter, one needs to exclude the effects from other lengths. If the incision diameter is sharp enough, the measured fracture energy will be only associated with the geometry of specimen, for example, in a pure shear specimen, Γ = W^*H. If the incision diameter is large enough, the stress state around the incision tip approaches uniaxial tension. The specimen has no stress concentration, and will rupture when all material particles reach W^*. Based on our analysis, the linear relation, Γ = W^*D, holds when Γ₀/W^* << D << H.

The fractocohesive length has been associated with the flaw-sensitivity length under monotonic loads^[11,12] and cyclic loads^[13], the transition thickness in peeling test^[14], the cavitation/fracture transition of soft materials^[15], as well as the flaw-sensitivity of hydrogels with dynamic covalent bonds^[16]. In this paper, we correlate the transition diameter of the incision with the fractocohesive length.

EXPERIMENTAL

In this paper we choose the polyacrylamide/Ca-alginate hydrogel as a model material, which has a high fracture toughness and insensitive to flaws^[11]. The hydrogel was synthesized by one-step method as follows^[17]. First, 1.74 M acrylamide (AAM, Aladdin), 0.48 mM N,N’-methylenebisacrylamide (MBAA, Aladdin), 6 mM ammonium persulfate (APS, Aladdin) and sodium alginate (Aladdin) (sodium alginate to acrylamide weight ratio is 1:6) were dissolved in deionized water and mixed evenly. Next, calcium sulfate (CaSO₄, Macklin) (CaSO₄ to sodium alginate weight ratio is 0.136:1) and N,N,N’,N’-tetramethylethylenediamine (TEMED, Aladdin) (TEMED to AAM weight ratio is 0.0025:1) were added. The mass fraction of water was 86%. The precursor solution was poured into a reaction vessel made of two parallel glass sheets separated by a 0.5 mm thick silicone spacer. The thermally initiated radical polymerization was carried out at 20 ℃ for 24 h. The mechanical property of polyacrylamide/Ca-alginate hydrogels is significantly affected by the synthesis process^[17]. The fracture energy reported in literature ranges from 200 ~ 8,500 J/m². We fix the process of material preparation to ensure the consistency of experimental results.

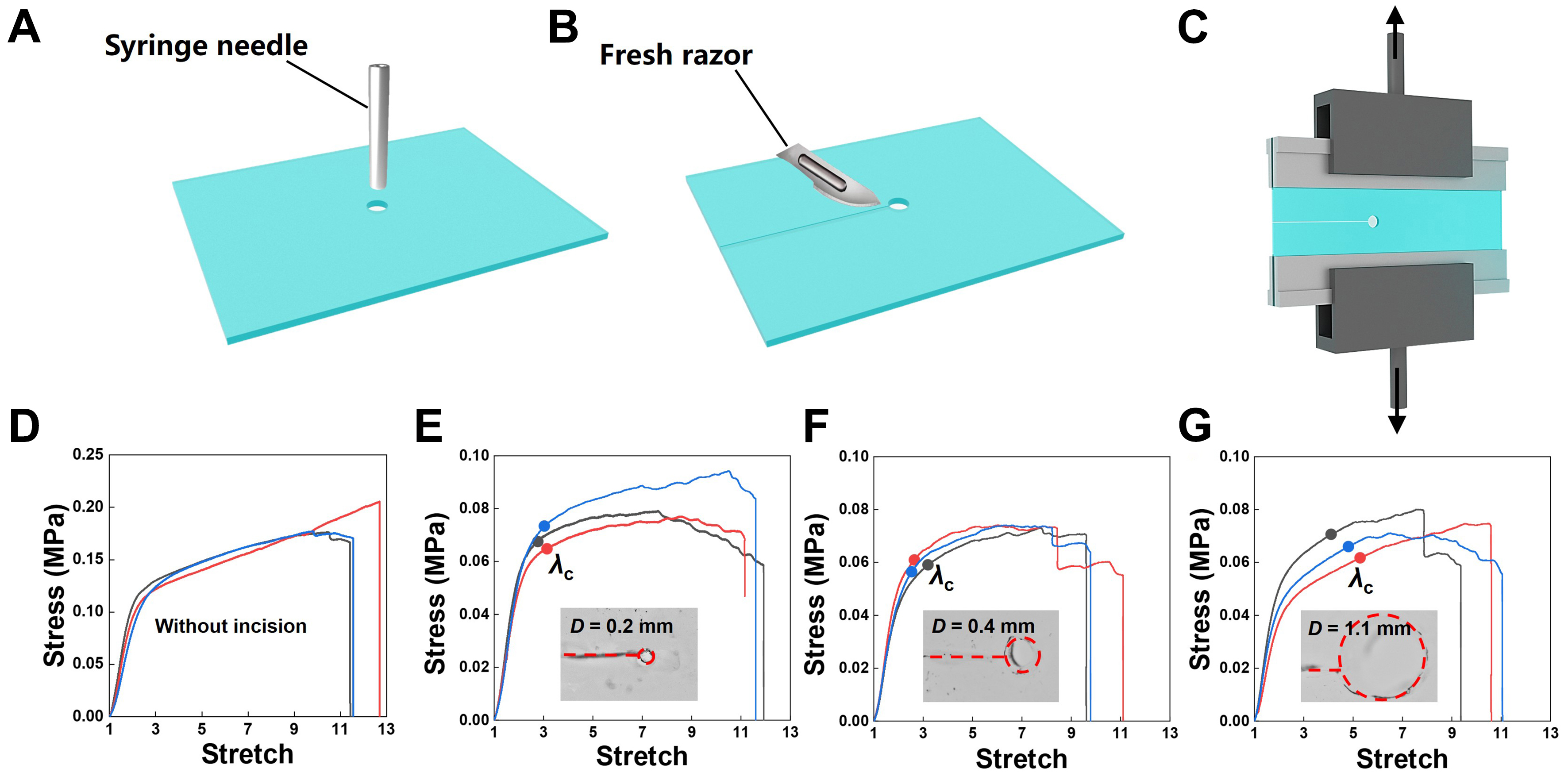
In this paper, we simplify incision tip as a circle and the circle’s diameter is the only characteristic length of incision tip. The specimens with 9 different incision diameters within the range of 0.15 ~ 2.5 mm were prepared as follows. A sheet of polyacrylamide/Ca-alginate hydrogel with 0.5 mm thickness was punctured into several rectangular specimens. Hollow syringe needles with different diameters were used to introduce circular holes in the specimen [Figure 2A]. Cracks were then introduced using a fresh razor from the edge of the holes [Figure 2B]. The total length of the crack and the circular hole was fixed as 20 mm. For each incision diameter, three specimens were prepared. The diameters of each individual specimen were measured using optical microscope (WK02K). We also prepared a cracked specimen without circular holes, representing the sharpest incision achievable. The diameter of this incision could not be identified by the optical microscope, indicating the tip diameter is below the microscope’s resolution of 3.75 μm. In principle, the smallest incision diameter is the mesh size of the hydrogel network, which is much smaller than the diameter of circular holes (~mm). In this case, to distinguish the sharpest incision from those with circular holes, we simply write the sharpest incision diameter as D = 0.

Figure 2. Measure the fracture energy of polyacrylamide/Ca-alginate hydrogel specimens containing incisions of different diameters. (A) Introduce a circular hole to a sheet of hydrogel; (B) Cut a crack from the edge of the hole; (C) Pure shear fracture test; (D) The stress-stretch curve of pure shear specimens without incision; (E-G) The stress-stretch curves of specimens with incision diameters D = 0.2, 0.4 and 1.1 mm. The insets show the incision tips observed by an optical microscope.

We used the pure shear configuration to measure the fracture energy of hydrogel specimens [Figure 2C]. Polymethyl methacrylate sheets were adhered to the specimens using cyanoacrylate to restrict the horizontal deformation. The effective dimensions of the pure shear specimen were 50 mm in length, 10 mm in height and 0.5 mm in thickness. The grippers only contact the sheets and avoid direct contact with the specimen, thereby preventing the specimen from breaking at the clamping point. The specimens were loaded on a tensile machine (SHIMADZU AGS-X) at a stretch rate of 0.03 s^-1. The stress-stretch curves of specimens with D = 0, 0.2, 0.4 and 1.1 mm are plotted in [Figure 2D-G]. Stress, s, is defined as the applied force divided by the sectional area in the undeformed state. Stretch, λ, is defined by the current length between two grippers divided by its reference length. Since the incision tip of polyacrylamide/Ca-alginate hydrogels usually blunts during the loading process, a vertical black line was marked near the incision tip prior to loading. This helps eyes to capture the rupture behavior at incision tip during the loading process. As the load increased, rupture was identified when the black line was observed to separate into two parts and the critical rupture stretch λ_c was recorded. The fracture energy Γ is calculated as

where W(λ_c) is the energy density, calculated as the area under the stress-stretch curve of the pure shear specimen without incision [Figure 2D] and H is the height of pure shear specimen.

RESULTS AND DISCUSSION

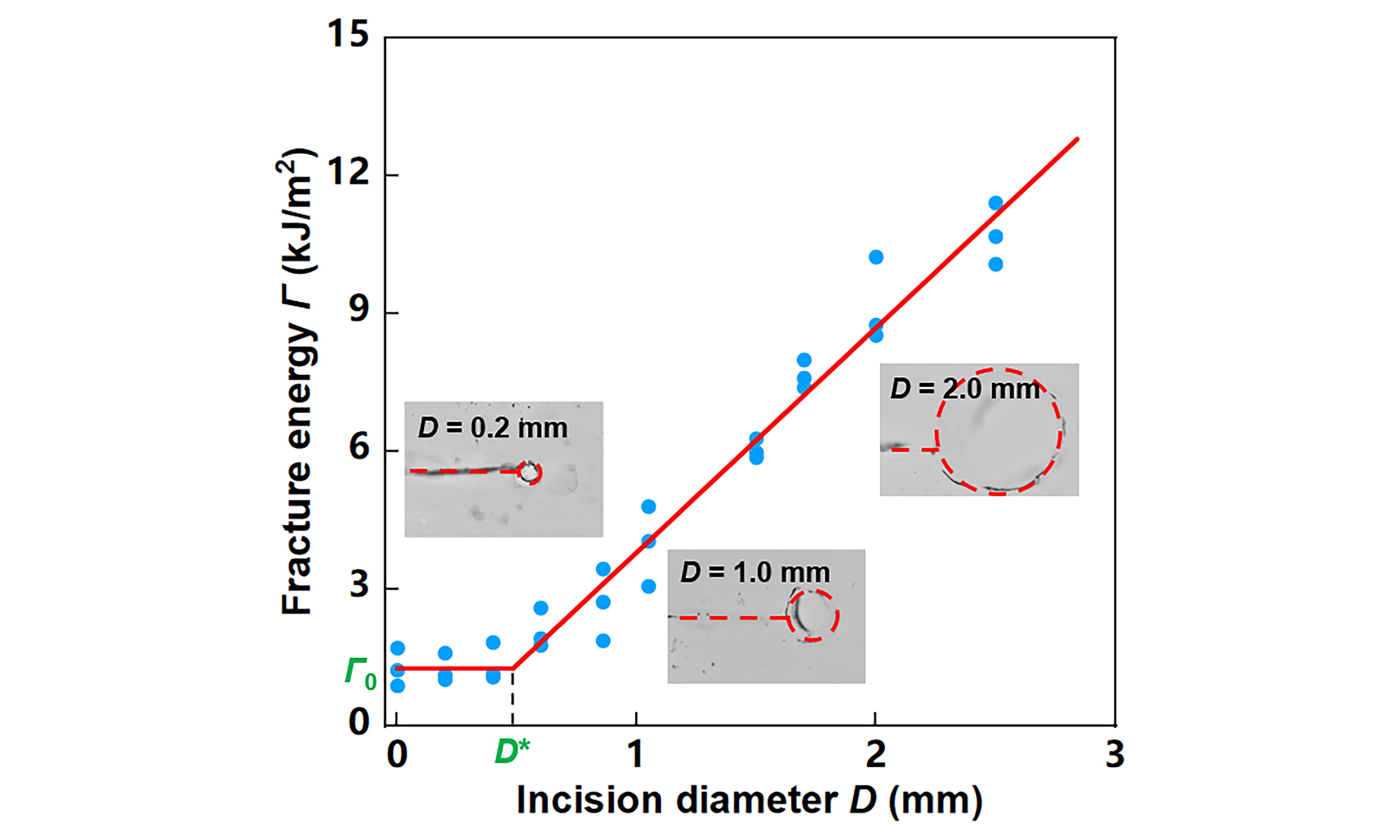
Figure 3 plots the measured fracture energy Γ (dots) as a function of the incision diameter D. For small incision diameters, Γ is nearly constant. For large incision diameters, Γ increases with D. The results agree with the hypothesis depicted in Figure 1B. The left three sets of data are fitted to a horizontal line, Γ = Γ₀. The right seven sets of data are fitted to an inclined line, Γ = k(D-D^*) + Γ₀. The two lines intersect at the transition diameter, D^*. The fitting gives Γ₀ = 1,262 J/m², k = 4.89 × 10⁶ J/m³ and D^* = 0.48 mm. Our analysis indicates that the plateau fracture energy in the Γ-D curve corresponds to the intrinsic material constant Γ₀. Furthermore, the transition diameter D^* is expected to be on the order of the fractocohesive length Γ₀/W^*. To validate this hypothesis, we will measure the work of fracture W^* and calculate the fractocohesive length Γ₀/W^* of polyacrylamide/Ca-alginate hydrogels.

Figure 3. The measured fracture energy Γ as a function of incision diameter D. Ten sets of data are plotted as dots. The left three sets of data are fit to a horizontal line, Γ = Γ₀. The right seven sets of data are fit to an inclined line, Γ = k(D-D^*) + Γ₀. The two lines intersect at a critical length D^*. When D < D^*, Γ is independent of D; When D > D^*, Γ linearly increases with D.

According to the relationship Γ = W^*D, the slope of the linear fit, k, should correspond to the material’s work of fracture. The work of fracture is regarded as a material constant. During the uniaxial tensile test, the specimen usually ruptures at the gauge region. The area under the stress-stretch curve represents the work of fracture of the specimen. However, during the pure shear test of an unnotched specimen, the specimen usually ruptures at the clamped region due to the complicated stress state in the clamped region. The rupture behavior in the clamped region can be influenced by the adhesive between the sheet and the specimen. Therefore, the uniaxial tensile test, rather than the pure shear test, is chosen to measure the work of fracture in this work.

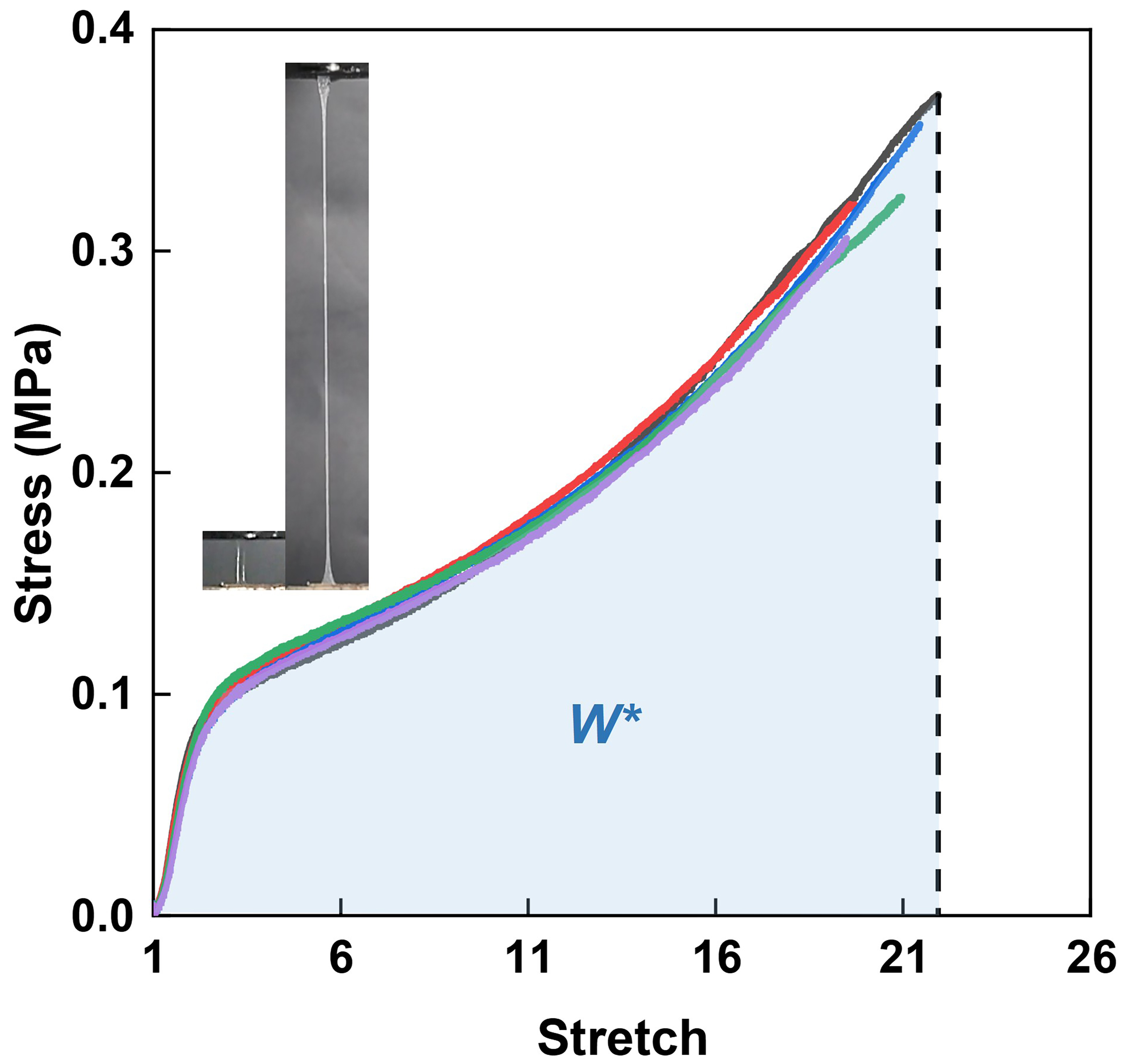
The work of fracture for polyacrylamide/Ca-alginate hydrogels was measured using uniaxial tension tests [Figure 4]. The specimens were prepared as dumbbell-shaped specimens with a width of 2 mm, a thickness of 0.5 mm, and a gauge length of 12 mm. The polyacrylamide/Ca-alginate hydrogel is a typical rate-dependent material^[17]; its mechanical properties can be significantly affected by the stretch rate. To avoid the effect of stretch rate, we fix the stretch rate of uniaxial tensile test and pure shear test as 0.03 s^-1. The work of fracture of specimens was determined by integrating the area under the entire stress-stretch curves [Figure 4]. Five specimens were tested, yielding work of fracture values of 4.09 × 10⁶ J/m³, 3.87 × 10⁶ J/m³, 3.70 × 10⁶ J/m³, 3.38 × 10⁶ J/m³ and 3.15 × 10⁶ J/m³. The stress-stretch curves of the five uniaxial tensile specimens are consistent, but the critical stretch of each specimen is slightly different. This variation of critical stretch can be attributed to the presence of defects in the specimens. Given that defects in fabricated specimens are inevitable, we select the highest measured work of fracture value as the hydrogel’s inherent constant to best approximate its true fracture energy. The measured work of fracture, 4.09 × 10⁶ J/m³, is comparable to the slope of the linear fit in Figure 3, k = 4.89 × 10⁶ J/m³. The transition diameter D^* was obtained through linear fit to be 0.48 mm. The fractocohesive length was calculated as Γ₀/W^* = 0.31 mm. The difference between the transition diameter D^* and the fractocohesive length Γ₀/W^* can be attributed to the existence of a coefficient between the two lengths. This coefficient is derived from the coefficient between the transition diameter D^* and the size of fracture process zone upon rupture.

Figure 4. Measure the work of fracture of the polyacrylamide/Ca-alginate hydrogel using uniaxial tension. The highest measurement value of work of fracture is regarded as the inherent constant of the hydrogel considering the inevitable defects in the fabricated specimens.

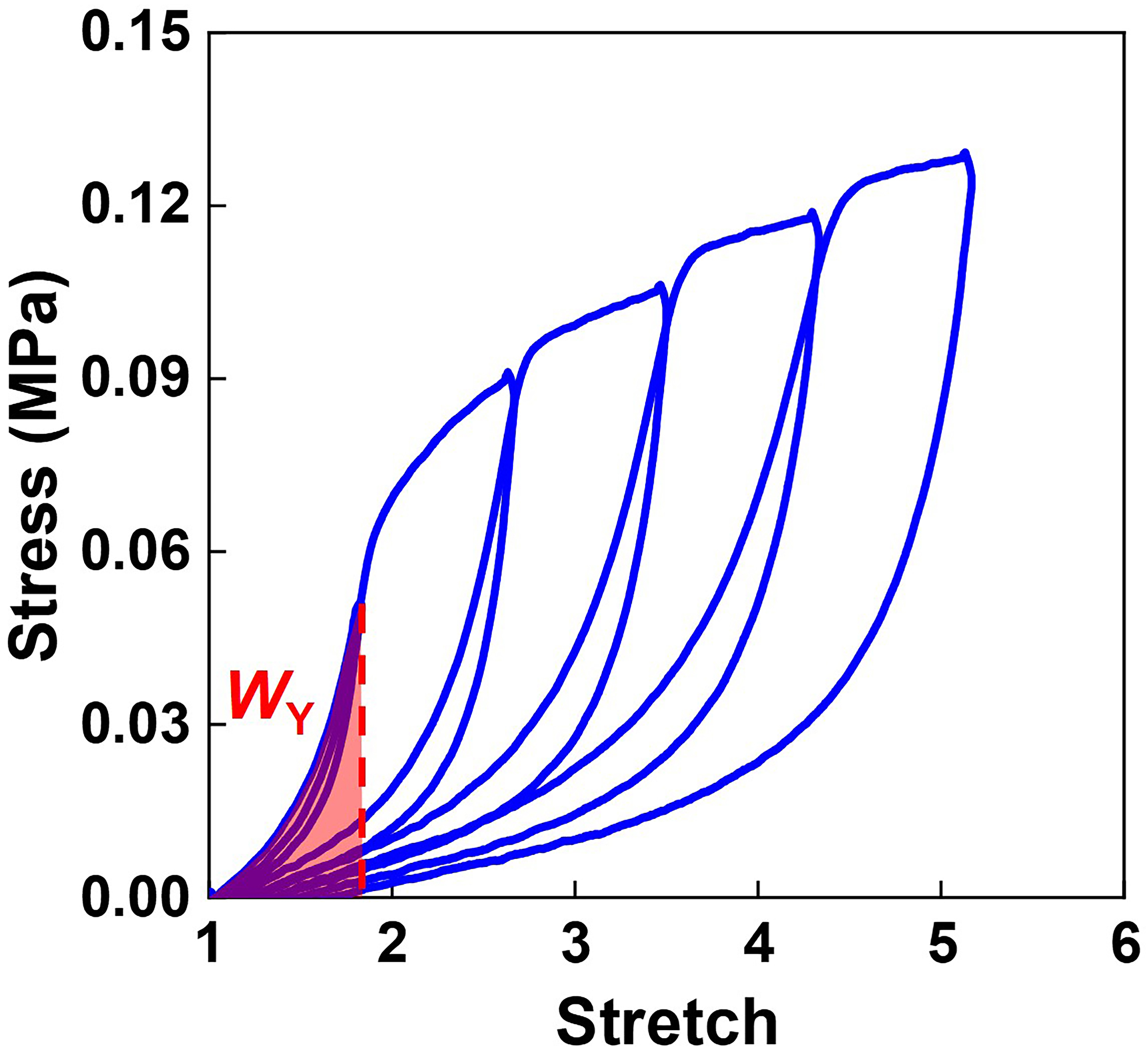
To assess the inelasticity of the material, a dumbbell-shaped specimen was subject to 5 cycles of loading and unloading [Figure 5]. The stretch ratio was also fixed at 0.03 s^-1. The hysteresis observed in the stress-stretch curve indicates significant inelasticity in the polyacrylamide/Ca-alginate hydrogel under large deformation. We individually define the elastic limit σ_Y as the stress level at which the hysteresis ratio remains below 10%. The work of yielding, W_Y, was determined by integrating the area under the stress-stretch curve until elastic limit σ_Y. The elastic limit σ_Y was found to be 0.05 MPa, and the work of yielding, W_Y, was calculated as 1.67 × 10⁴ J/m³. The elastic limit σ_Y = 0.05 MPa in Figure 5 is much lower than the rupture stress 0.36 MPa in Figure 4. This suggests that inelasticity prevails on a large scale, potentially encompassing the entire specimen.

Figure 5. The hysteresis curve of the polyacrylamide/Ca-alginate hydrogel. The elastic limit σ_Y is defined as the stress level under which the hysteresis ratio is less than 10%. The work of yielding W_Y is calculated by integrating the area under the stress-stretch curve until the elastic limit σ_Y.

The definition of the elastic limit for materials with nonlinear large deformation is usually arbitrary. Here 10% hysteresis was selected subjectively to determine σ_Y for the hydrogel. The determination of σ_Y is used to calculate the work of yielding W_Y and compare it with the work of fracture W^*. The elastic limit can alternatively be defined using a 5%, 1%, or other percentage. For a 5% hysteresis threshold, the elastic limit (σ_Y) is 0.02 MPa, with a corresponding energy density (W_Y) of 5.84 × 10³ J/m³. In contrast, for a 1% hysteresis threshold, σ_Y remains 0.02 MPa, but W_Y decreases to 7.31 × 10² J/m³. Although a 10% hysteresis threshold may be considered too large for defining the elastic limit, the difference between W_Y and W^* already spans three orders of magnitude. This contrast illustrates the significant difference between fractocohesive length and the scale of inelasticity.

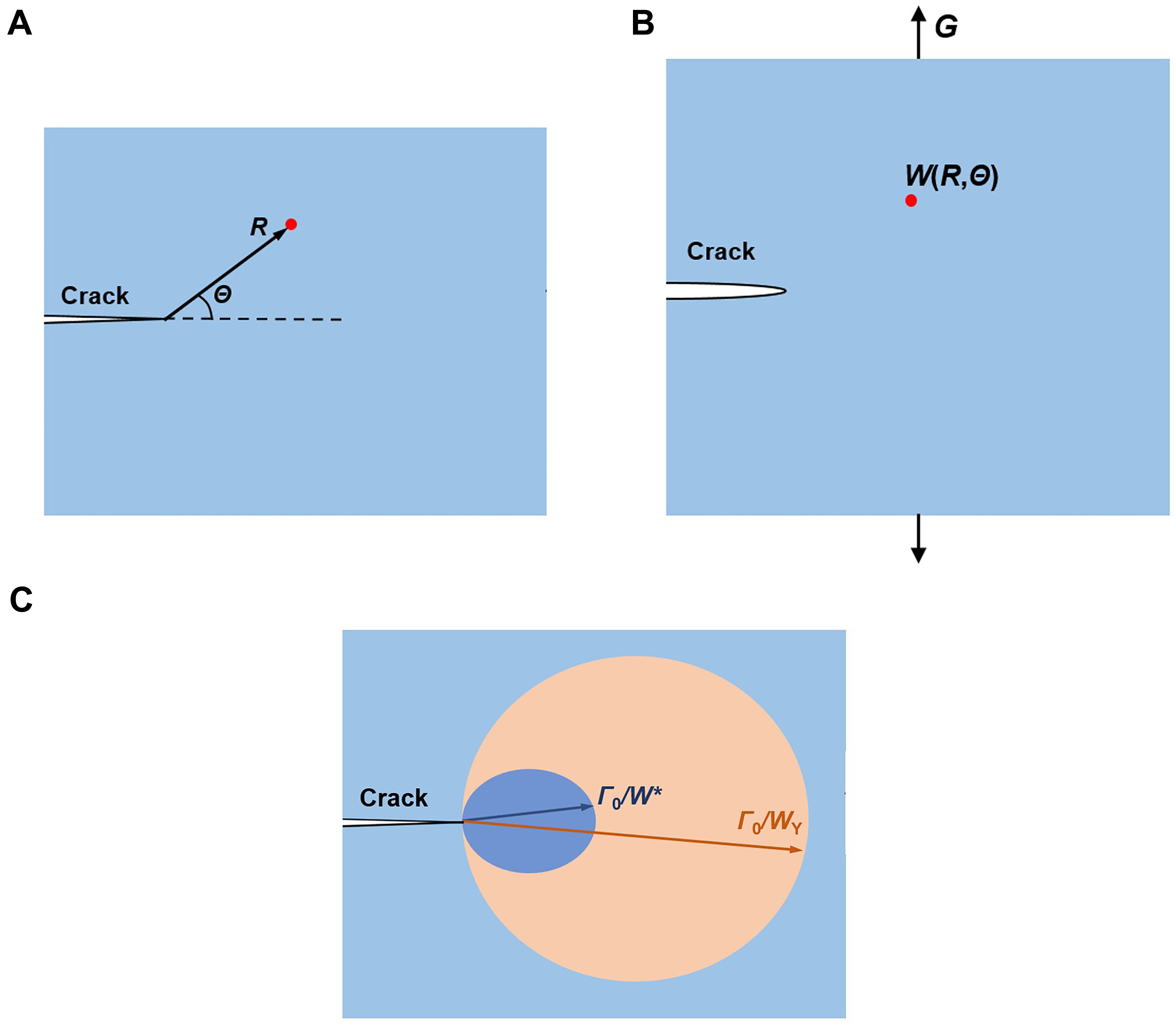
To compare the scale of inelastic zone with the fractocohesive length, we review the concept of crack tip field in the theory of fracture mechanics. Consider a polyacrylamide/Ca-alginate hydrogel specimen containing an ideally sharp crack. In the undeformed state, a material particle of the body can be labeled by polar coordinates (R, Θ) centered at the crack tip [Figure 6A]. In the deformed state, the same material particle (R, Θ) moves to a different place in space [Figure 6B]. The applied load can be represented by energy release rate G, which is defined by the elastic energy released from the system per unit area of crack extension. In the deformed state, the deformation field of the body is a field of the coordinates of material particles in the undeformed state. Meanwhile, the field of energy density is a function W (R, Θ).

Figure 6. Comparison between the scale of fractocohesive length and the scale of inelastic zone. (A) In the undeformed state, a material particle is labeled by polar coordinates (R, Θ) centered at the tip of the crack; (B) In the deformed state, the applied load is represented by the energy release rate G. The field of energy density is a function W (R, Θ). For a given material point, its distance R from the crack tip is the only length scale. The field of energy density W scales with the energy release rate G as W ~ G/R (light blue region); (C) The comparison between the fractocohesive length (dark blue region) and the scale of inelastic zone (orange region).

In our case, the hydrogel is loaded without unloading. Following the procedure of dealing with large-scale inelastic fracture of elastic-plastic material, we approximate the deformation field to the elastic field. When the incision tip diameter D approaches zero, for any constitutive model of elasticity, the field of energy density scales with the energy release rate as

Here f represents a dimensionless function dependent only on the polar angle Θ, not on R. Dimensional considerations establish the scaling relation W ~ G/R: The field of energy density, W, has units of energy per unit volume, whereas the energy release rate, G, has units of energy per unit area. The governing elastic equations and the boundary conditions for a semi-infinite crack in an infinite body both lack a characteristic length scale. For a given material point, its distance R from the crack tip is the only length scale. As a result, the field of energy density W scales with the energy release rate G as W ~ G/R.

Upon the rupture of the specimen, the energy release rate G reaches the fracture energy Γ₀, and the energy density W in the fracture process zone attains the work of fracture W^*. Consequently, the size of the fracture process zone scales with Γ₀/W^*. Outside the fracture process zone, the inelasticity prevails in the region that attains the work of yielding W_Y. Similarly, the size of the inelastic zone scales with Γ₀/W_Y. For the polyacrylamide/Ca-alginate hydrogel, W_Y is 1.67 × 10⁴ J/m³, which is much smaller than the work of fracture W^* (4.09 × 10⁶ J/m³). The scale of inelastic zone Γ₀/W_Y is calculated as 75.6 mm, as shown in Figure 6C in the orange region. The fractocohesive length Γ₀/W^* is calculated as 0.31 mm, as shown in Figure 6C in the dark blue region. The light blue region outside represents the elastic field, which corresponds to the relation W ~ G/R. As a result, the scale of inelastic zone Γ₀/W_Y is three orders of magnitude larger than the fractocohesive length Γ₀/W^*. A similar phenomenon has been observed in poly (lactic acid)^[18].

In the linear elastic fracture mechanics for a metal, the plastic zone size r_p is calculated by^[19]

where G is the energy release rate, and W_Y is the work of yielding. In metals, the fracture process zone is typically considered to scale with the plastic zone. However, our experimental results indicate that these two scales differ significantly in a polyacrylamide/Ca-alginate hydrogel. Specifically, at the onset of yielding, hysteresis is minimal, energy dissipation remains incomplete, and the material is far from rupture. In contrast, the work of fracture encompasses the total energy dissipated during the entire loading process, while the fracture process itself occurs within the fracture process zone, which scales with the fractocohesive length Γ₀/W^*. Consequently, the fractocohesive length is the characteristic length governing fracture behavior in stretchable materials. In our study, the fractocohesive length effectively explains the transition point observed in the dependence of measured fracture energy on incision tip diameter D.

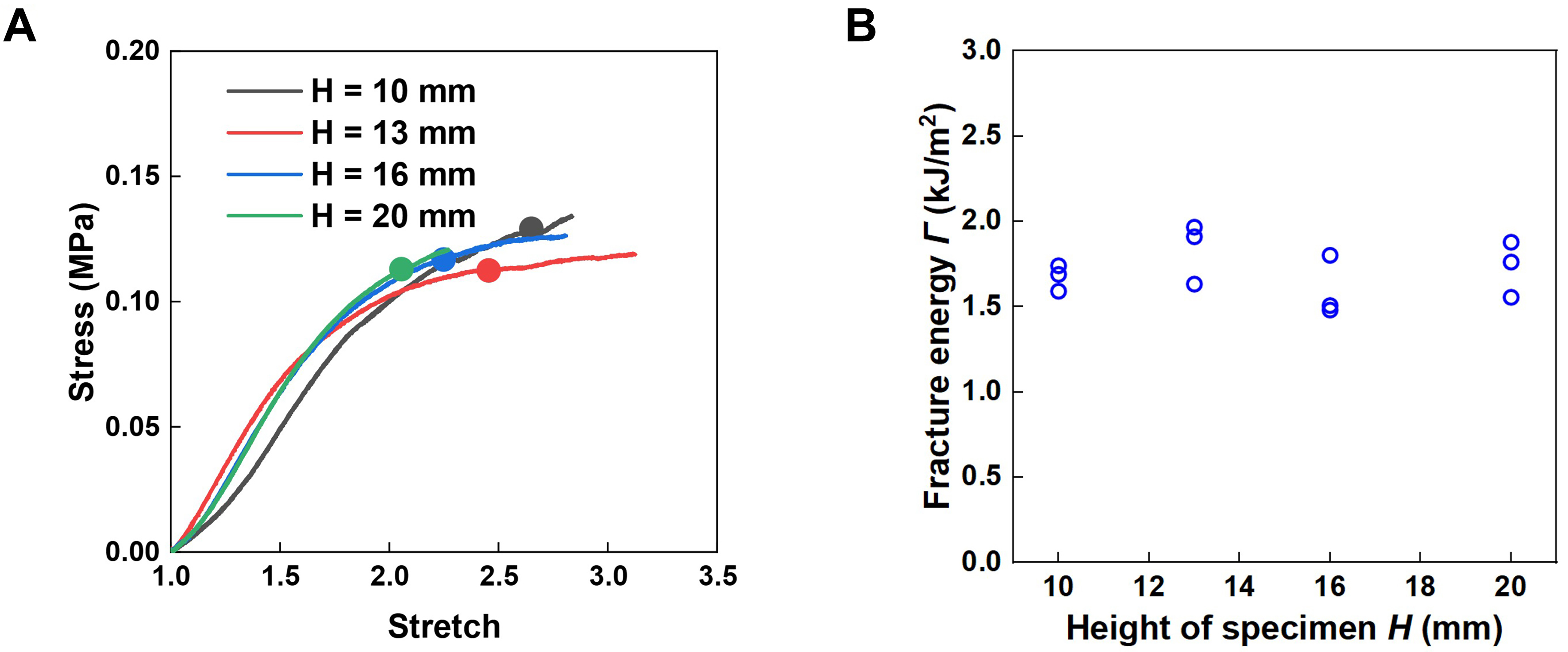
Begley and Landes experimentally measured the fracture energy of metals under large-scale inelasticity conditions, and found that fracture energy is constant, independent of the type and size of specimen^[20,21]. Following this spirit, here we identify whether the fracture energy of the polyacrylamide/Ca-alginate hydrogel depends on the characteristic length of pure shear configuration, i.e., the height of specimen H. We tested the pure shear specimens with four different heights ranging from 10 ~ 20 mm. The ratio between the width and the height was fixed at 5. The thickness of specimens was 0.5 mm. To exclude the effect of incision curvature on the measured fracture energy, we introduced the incisions of all the pure shear specimens using a fresh razor. Namely, all specimens had an incision diameter of D = 0. The calculation of fracture energy Γ followed the same method as given above. The stress-stretch curves of pure shear specimens with height H = 10, 13, 16 and 20 mm are shown in Figure 7A. The experimental results indicate that the specimens with different heights have similar stress-stretch curves, but the critical stretch decreases as the height H increases. The fracture energy Γ of each specimen is calculated and plotted in Figure 7B. The Γ-H plot illustrates that the measured fracture energy is roughly independent of the specimen height. For each height H, three specimens were tested.

Figure 7. The measured fracture energy is independent of specimen height. (A) Stress-stretch curves of pure shear specimens with different heights H = 10, 13, 16 and 20 mm; (B) The measured fracture energy as a function of specimen height.

According to our analysis, to study the effect of incision diameter, one needs to exclude the effects from other lengths, especially the geometric length. Therefore, the independence of the measured fracture energy Γ on the specimen height H should be verified to ensure that the incision diameter is the only characteristic length. The experimental results in Figure 7B show that the measured fracture energy is nearly a constant for specimens with heights ranging from 10 ~ 20 mm. This confirms that the specimen height we used (H = 10 mm) was sufficient to investigate the influence of incision curvature on measured fracture energy.

The specimen height we selected significantly exceeds the fractocohesive length but remains smaller than the scale of inelasticity. For the polyacrylamide/Ca-alginate hydrogel, the scale of inelasticity is calculated as 75.6 mm - substantially larger than the height range (10 ~ 20 mm) of our pure shear specimens. This implies that the entire specimen undergoes inelastic deformation upon rupture. If the scale of inelasticity were the characteristic length governing fracture energy measurement, the measured fracture energy should scale proportionally with specimen height. However, our experimental results demonstrate that the measured fracture energy is independent of specimen height. This finding confirms that when the specimen’s geometric dimensions significantly exceed the fracture process zone size (~Γ₀/W^*), the measured fracture energy represents a material constant. Furthermore, these results verify that the fractocohesive length, not the scale of inelasticity, serves as the characteristic length describing the hydrogel’s fracture behavior. This observation also provides a consistency check for the previously reported transition behavior.

CONCLUSIONS

This paper investigates the effect of incision curvature on fracture energy measurement in soft materials. This study selects polyacrylamide/Ca-alginate hydrogel as the example. The fracture energy was measured by a pure shear configuration. The experimental results show that, for small incision tip diameters, the measured fracture energy is independent of the incision diameter and instead reflects the intrinsic fracture energy of material. For larger incision tip diameters, the fracture energy becomes proportional to the incision tip diameter, with the slope representing the material’s work of fracture. This transition occurs at an incision diameter comparable to the fractocohesive length. This length scale differs from the inelastic zone scale. The difference between the fractocohesive length and the inelastic zone scale spans three orders of magnitude. The fractocohesive length explains the transition behavior in the effect of incision curvature on fracture energy measurement for polyacrylamide/Ca-alginate hydrogels. The results of this paper will be helpful for establishing standards for measuring fracture energy of soft materials.