Phase-field simulation of electrocaloric effect in textured Ba0.8Sr0.2TiO3 polycrystalline ceramics
Abstract
Textured ceramics exhibit a reduced coercive field, and when aligned in the same direction as the spontaneous polarization, they enhance the adiabatic temperature change (ΔT) of the material. In this paper, we employ a polycrystalline phase-field model to analyze the solid solution Ba0.8Sr0.2TiO3 (BST80) with a <001> orientation, alongside randomly oriented polycrystals, aiming to investigate the influence of texturing on the electrocaloric effect (ECE) performance. We examine six distinct groups characterized by varying grain orientation angles for the randomly oriented polycrystals for hysteresis loop calculations. Utilizing Maxwell's relations, we compute the ECE for the randomly oriented BST80 polycrystal and the <001>-textured BST80 polycrystal across different electric field strengths. The findings indicate that the ∆T achieved with the <001>-textured BST80 polycrystal surpasses that of the randomly oriented BST80 polycrystal. Furthermore, the temperature at which the maximum ΔT occurs for the <001>-textured BST80 polycrystal is observed to be shifted to higher values compared to the randomly oriented variant. The observed enhancement of ECE in BST80 polycrystalline ceramics due to texturing offers valuable insights and foundational knowledge for future theoretical and experimental investigations.
Keywords
INTRODUCTION
While texturing can enhance piezoelectric performance[1], only a limited number of recent studies have investigated its effect on the electrocaloric performance of ceramic materials[2,3]. Research indicates that for <111> oriented 0.90Pb(Mg1/3Nb2/3)O3-0.10 PbTiO3 (PMN-PT) ceramics[3], applying an electric field parallel to the direction of spontaneous polarization increases the adiabatic temperature change (ΔT) when texturing is also aligned in that direction. In lead-free ferroelectrics, Na0.5Bi0.5TiO3 (NBT)-based ceramics have been extensively studied due to their electrocaloric performance. However, while there has been considerable research on their electrocaloric properties, there is a lack of studies examining how texturing affects the electrocaloric performance in NBT-based systems. Texturing in NBT-based materials is primarily achieved through a template grain growth process, which aims to enhance their piezoelectric characteristics[4-8]. This process involves arranging highly anisotropic particles (templates) among fine matrix particles. After heat treatment, these templates grow while preserving their arrangement, resulting in a textured microstructure. Among various template materials, NBT templates are effective in minimizing lattice mismatch, crystal structure, and compositional differences between the matrix and template materials[4]. Maurya et al. successfully created texture in NBT-BT ceramics using <100> oriented NBT templates, which improved the piezoelectric response[4]. Their research also revealed that textured samples exhibit a lower coercive field and facilitate easier domain wall motion compared to non-textured ceramics. In NBT-based materials, 0.82NBT-0.18KBT ceramics have been thoroughly studied for their outstanding piezoelectric properties, largely due to the presence of quasi-homogeneous phase boundaries that allow for the coexistence of tetragonal and rhombohedral phases, resulting in significant polarization and a high piezoelectric coefficient d33[9,10]. The electrocaloric performance of 0.82NBT-0.18KBT ceramics shows promising application potential. Initially, Cao et al. found that at 80 kV·cm-1, the transition temperature from the ferroelectric to paraelectric phase was 340 K, with a ΔT of 1.62 K, leading to an electrocaloric strength (ΔT/ΔE) value of 0.212 × 10-6 K·m·V-1[11]. Additionally, Goupil et al. conducted a more comprehensive study on the electrocaloric properties of 0.82NBT-0.18KBT using both direct and indirect measurement techniques, reporting a higher depolarization temperature (around 423 K) and greater electrocaloric strength: at 433 K, ΔT was measured at 0.73 K at 22 kV·cm-1, with an electrocaloric strength of 0.33 × 10-6 K∙m·V-1, comparable to the best lead-free materials[12]. To date, NBT-KBT has been textured using three different templates, including BaTiO3 (BTO), SrTiO3, and NaNbO3, with BTO templates demonstrating higher field-induced strain in the textured ceramics[13].
Experimental findings indicate that the orientation and complex phase transitions of 0.71PMN-0.29PT single crystals significantly influence their maximum electrocaloric effect (ECE) temperature[14]. Various (Pb0.97La0.02)(Zr0.73Sn0.22Ti0.05)O3 films with specific orientations have been prepared, demonstrating that <111> oriented films can achieve a ΔT of 28.1 K at room temperature[15]. Current studies indicate that texturing can enhance the electrocaloric performance in the PMN-PT system and reduce the coercive field in NBT-based ceramic materials. However, due to experimental limitations, these results cannot yet be applied to polycrystalline materials. Hamad et al. employed a theoretical phenomenological model to calculate the maximum adiabatic temperature change range for PMN polycrystalline ceramics with varying stoichiometric compositions[16]. Hou et al. investigated the effect of grain size on ECE performance in PbTiO3 polycrystalline ceramics using a phase-field method, discovering that larger-grain polycrystals exhibit greater temperature changes[17]. These studies underscore the significant role of grain orientation and structure in the ECE performance of ferroelectrics. The influence of grain orientation on the ECE performance of polycrystals remains uncertain due to the lack of models for polycrystal models with small grain sizes[18]. Therefore, developing a polycrystal model to analyze the effect of grain orientation on ECE performance is essential.
In single crystal and thin film systems, numerous simulations have been conducted on domain evolution during the ferroelectric transition and under applied electric fields[19-23], alongside some theoretical studies on the switching behavior of ferroelectric polycrystals[24-26]. These models generally assume that ferroelectric polycrystals consist of single-domain grain arrays. When the energy from the external field surpasses a critical threshold, ferroelectric or piezoelectric transitions will occur. Kim et al. introduced a continuum model to investigate the impact of grain boundaries on switching behavior within a one-dimensional framework[27]. Rödel et al. developed a micromechanical model to describe how grain orientation affects domain switching in ferroelectric ceramics with layered domain structures[28]. Recently, Zhang et al. presented phase-field models for domain switching in single crystals and bicrystals, indicating that the switching behavior is influenced by the orientation difference between the two half-crystals in bicrystals[29]. Research by Li et al. demonstrated that domain switching in grains is constrained by adjacent grains[30]. Choudhury et al. proposed a polycrystalline phase-field model to predict polarization switching and domain structure evolution in ferroelectric polycrystals under applied electric fields[31,32]. Nevertheless, none of the existing research examines the influence of ceramic texture on the microscopic analysis of ECE. The solid solution BaxSr(1-x)TiO3 offers a broad range of tunable TC transition temperatures and high dielectric constants due to varying doping ratios. Consequently, this research focuses on <001> oriented BaxSr(1-x)TiO3 as a template to investigate the effect of texturing on the ECE performance of BaxSr(1-x)TiO3 ceramics.
MATERIALS AND METHODS
To explain the domain structure and morphology of polycrystalline ferroelectric materials, it is essential to first introduce the order parameter η, which characterizes the orientation of the crystals. The local spontaneous polarization within each grain is referred to as PL. In a global coordinate system, the global spontaneous polarization order parameter P and the displacement field u are defined. Analyzing the time-dependent Ginzburg-Landau equation leads us to conclude that both the global polarization order parameter and the displacement field must adhere to the principles of energy relaxation minimization and mechanical equilibrium equations[33-36]. Furthermore, the electric displacement must also conform to the electrical equilibrium equation:
The total free energy of the system is composed of the following four energy terms:
With the incorporation of various grain orientations, the Landau polynomial expansion for the bulk free energy density must be formulated within a local coordinate system. The local Landau polynomial for the BaxSr(1-x)TiO3 system examined in this study can be represented as follows:
Among them, α1-α1123 represents the coefficient of the Landau energy term, while PL refers to the local spontaneous polarization of each grain within its respective local crystal coordinate system. To address the equations for thermodynamic and electrical equilibrium, it is essential to align the local coordinates with the global coordinate system. To achieve this, we define a spatial rotation matrix by introducing three Euler angles. The rotation matrix that transforms global coordinates into local coordinates can be expressed as:
As a result, the local spontaneous polarization can be calculated by applying a rotation matrix from the left to the global polarization.
To simplify the process, the gradient energy of the polycrystalline material is treated as the bulk energy of a single crystal system:
Given the varying orientations of the grains, the intrinsic strain orientation within each grain also differs. Consequently, the intrinsic strain can be defined as:
According to the well-known Maxwell relation
where ρ is the material density and CP is the specific heat capacity. E1 and E2 denote the start and end electric fields applied. To use this indirect measurement, the necessary treatment process is as follows. Firstly, the relationships between the polarization and the electric field at different temperatures should be tested over a certain temperature range. Secondly, the temperature dependence of polarization with the applied electric field can be obtained from the upper branches of the hysteresis loops for E > 0.
RESULTS AND DISCUSSION
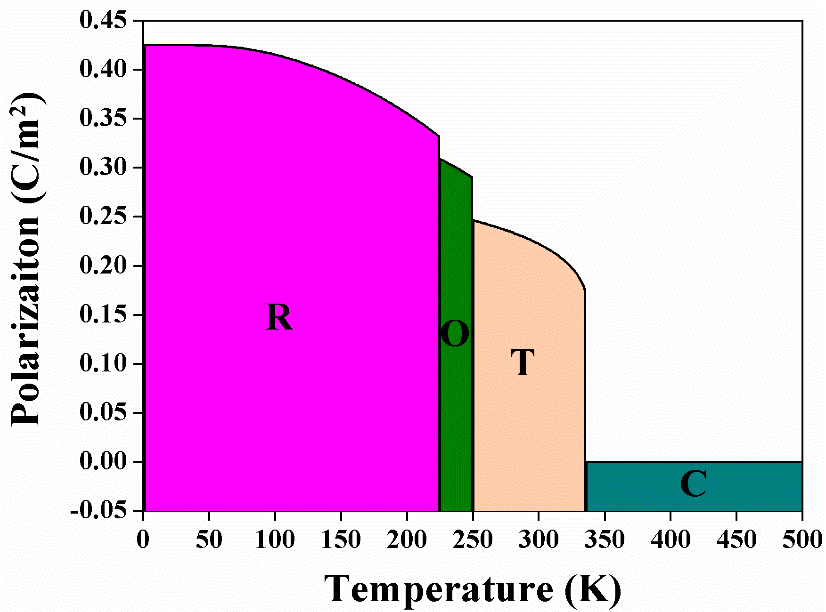
In this section focused on simulation calculations, we investigate the solid solution BaxSr(1-x)TiO3. To achieve a TC near room temperature, we employ Sr doping to modify the properties of BaxSr(1-x)TiO3. Following the phase diagram of Sr content in BaxSr(1-x)TiO3 and its correlation with TC, as proposed by Huang et al., we select a Sr doping ratio of 0.2[57]. The resulting temperature and phase structure phase diagram is illustrated in Figure 1, which shows that Ba0.8Sr0.2TiO3 (BST80) exhibits four phases throughout the temperature range: rhombohedral (R phase), orthorhombic (O phase), tetragonal (T phase), and cubic (C phase). This is similar to the temperature phase diagram of BTO, which also features these four phases, albeit with different temperature ranges for each. In the BST80 temperature phase diagram, the R phase predominates below 225 K, transitioning to the O phase as the temperature rises, with the O phase being confined to a narrow range of 25 K between 225 K and 250 K. The tetragonal T phase exists from 250 K to 335 K, and above 335 K, the material enters the paraelectric C phase. We focus on the T phase at room temperature as the optimal choice.
Figure 1. Phase diagram of the solid solution BaxSr(1-x)TiO3 with Sr content of 0.2, showing the temperature ranges for different phases (R, O, T, and C). R phase: rhombohedral; O phase: orthorhombic; T phase: tetragonal; C phase: cubic.
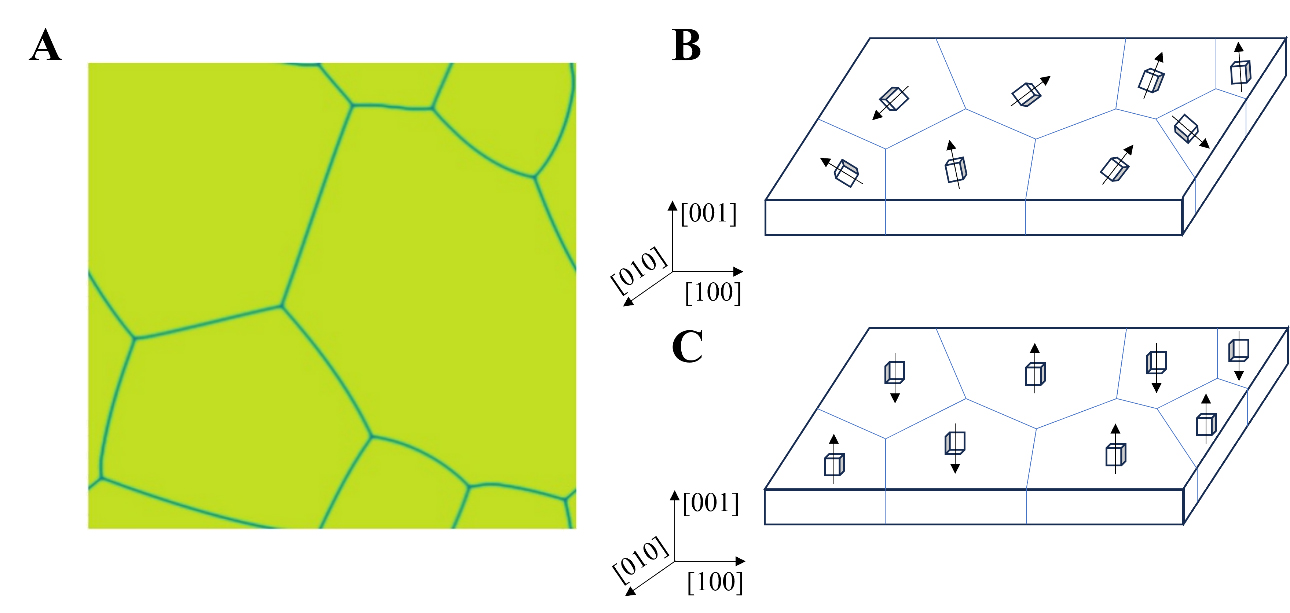
Based on this analysis, we proceed to select the T phase of BST80 that is stable at room temperature. To construct a polycrystalline model, we utilize a proprietary program developed within our research group to generate a polycrystalline framework. The thickness of the grain boundaries was constrained to 2 computational units, and the specific types of grain boundaries were not taken into account. The ferroelectric polarization within each grain is influenced by the differing orientation angles of the grains, resulting in a distribution of polarization directions throughout the polycrystalline framework; thus, periodic boundary conditions were employed in the simulation system. Furthermore, the polarization direction at the grain boundaries is determined by the polarization distribution between neighboring grains. Consequently, this study does not address the impact of grain boundary types on ECE. Our objective is to create a BST80 polycrystalline sample with dimensions of 256∆x × 256∆y × 1∆z, where ∆x = ∆y = ∆z = 1 nm. The framework for generating a stable polycrystalline model is illustrated in Figure 2A.
Figure 2. (A) The BST80 polycrystalline model framework; Schematic diagram of the BST80 polycrystalline model with (B) random orientation and (C) <001> orientation. BST80: Ba0.8Sr0.2TiO3.
To establish both <001>-oriented and randomly oriented BST80 polycrystalline models, we first construct the framework of the polycrystalline model based on the theoretical methodologies. By rotating individual grains, we modify their orientations. The specific characteristics of the randomly oriented and <001>-oriented BST80 polycrystalline models are illustrated in Figure 2B and C. In this study, we develop both <001>-oriented and randomly oriented BST80 polycrystalline models and apply a uniform electric field of uniform intensity along the [001] direction to examine ∆T in both models.
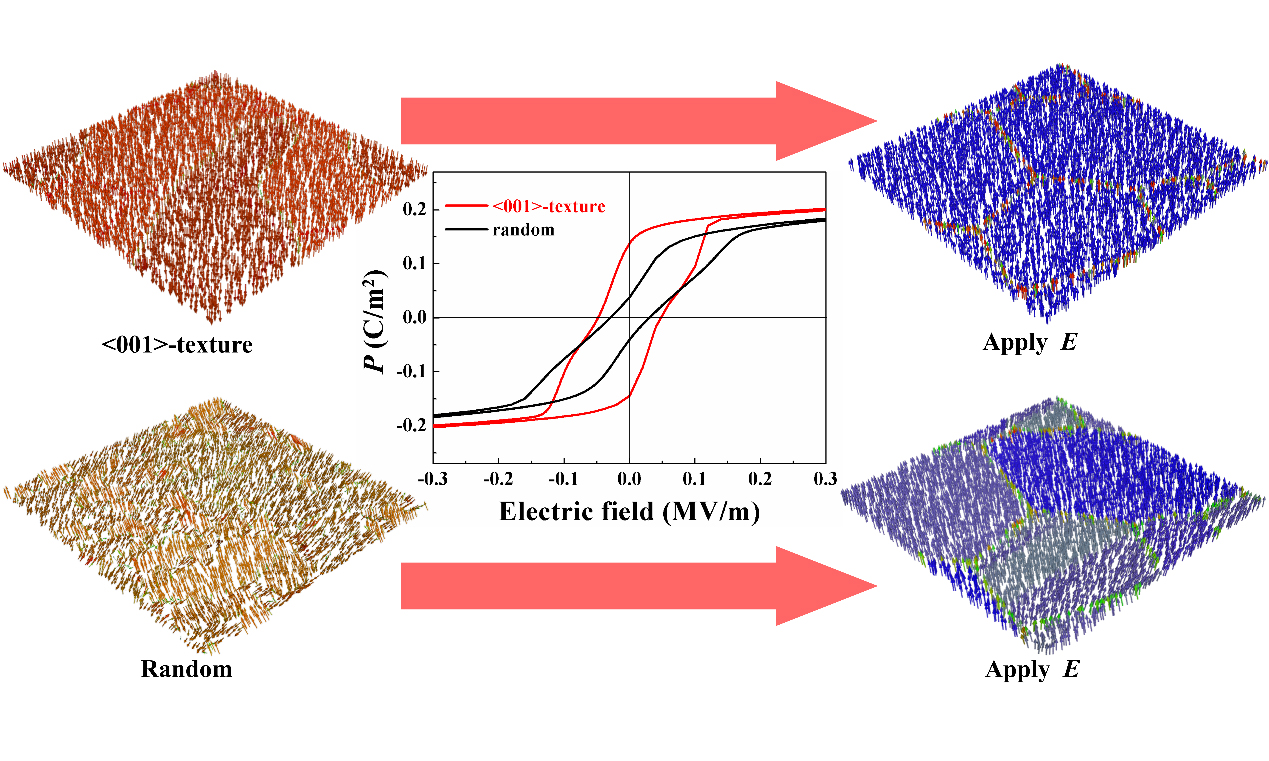
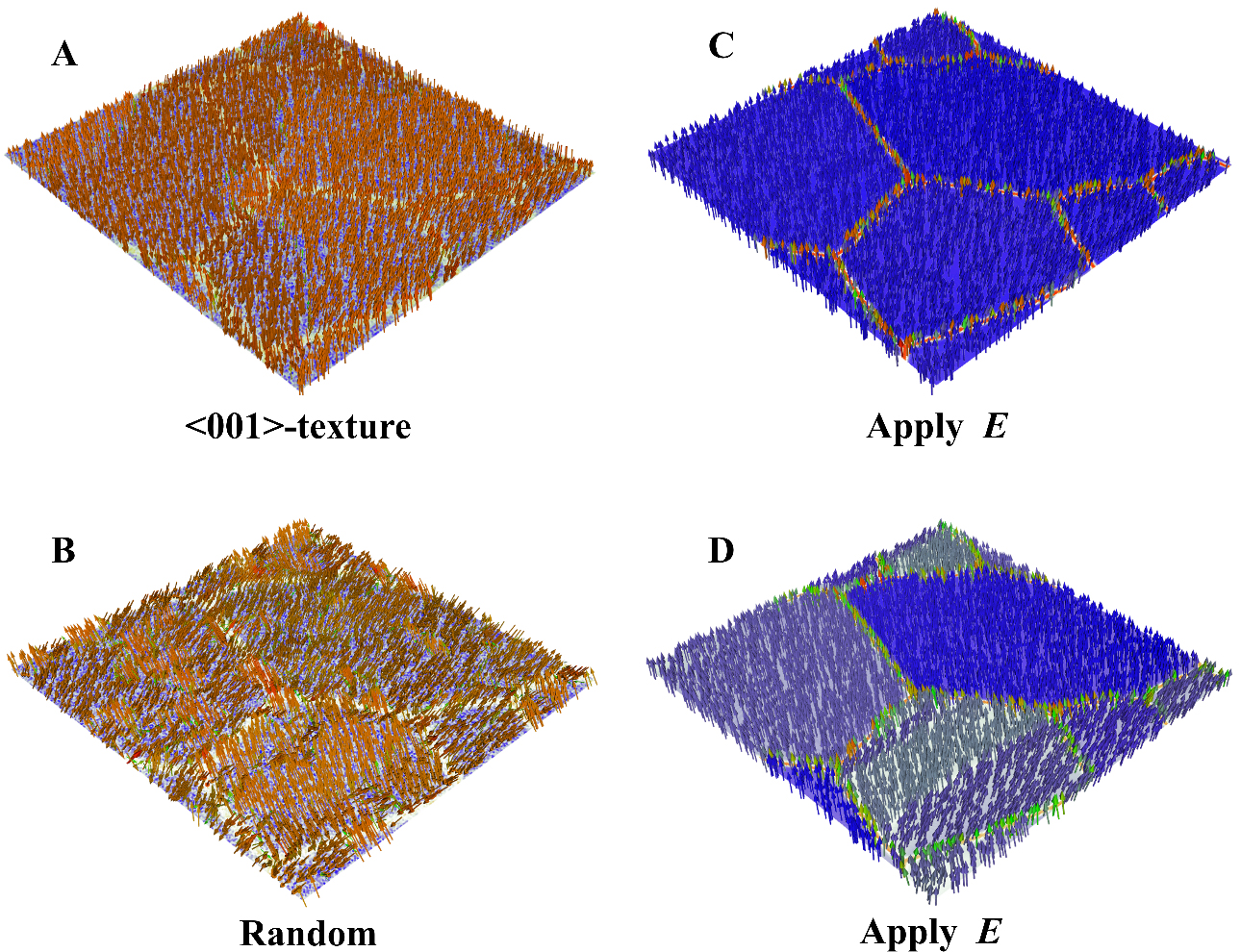
Through the analysis of the phase diagram of BST80 and the application of the previously established polycrystalline model framework, we generated two-dimensional samples of ferroelectric BST80 polycrystals exhibiting both randomly oriented and <001>-oriented, as illustrated in Figure 3A and B. Figure 3A depicts the states of ferroelectric polarization directed upwards along [001] and downwards along [00
Figure 3. The left side (A) and (B) represent the initial domain structure characterized by <001>-texture and random ceramics, while the right side (C) and (D) illustrate the domain structure under the influence of an applied electric field. The orientation of the arrows illustrated in the figure indicates the direction of polarization. The white contours in panels (A) and (B), along with the red arrows in panel (C) and the green arrows in panel (D), represent the polarization direction at the grain boundaries.
Figure 4. (A) The P-E loop curves of BST80 polycrystalline for sample 1, along with three sets of random orientation angles for samples 5, 6, and 7. The regions I-VI depicted in panel (B) illustrate the microscopic domain morphology at various phases of the P-E loop, encompassing scenarios both with and without the incorporation of textured ceramics, as shown in panel (A). The different colors observed within the ferroelectric domains represent the various types of domain structures, each characterized by distinct orientations. (C) The relationship curve between ΔT and temperature (T) generated by the BST80 polycrystalline under an electric field strength of 1 MV·m-1 for six sets of random orientation angles. BST80: Ba0.8Sr0.2TiO3; ΔT: temperature change.
For the randomly oriented BST80 polycrystal, we selected six groups of distinct grain orientation angles for polycrystal evolution: (-10°, -8°, -6°, -4°, 0°, 4°, 6°, 8°, 10°), (-20°, -15°, -10°, -5°, 0°, 5°, 10°, 15°, 20°), (-30°, -23°, -15°, -7°, 0°, 7°, 15°, 23°, 30°), (-40°, -30°, -20°, -10°, 0°, 10°, 20°, 30°, 40°), (-100°, -75°, -50°, -25°, 0°, 25°, 50°, 75°, 100°), and (-150°, -112°, -74°, -36°, 0°, 36°, 74°, 112°, 150°), as seen in Table 1. The six ferroelectric domain structures, labeled I-VI in Figure 4B, represent various evolutionary states of textured and random polycrystals subjected to different electric fields, as illustrated in Figure 4A. The application of the P-E Loop, combined with the analysis of ferroelectric domain evolution topography, demonstrates that textured polycrystals exhibit a lower coercive field and reduced residual ferroelectric polarization compared to their random polycrystal counterparts. Furthermore, textured polycrystals can achieve a higher maximum polarization value. However, for the three groups of random orientation angles depicted in Figure 4A, the hysteresis loops of the BST80 polycrystal largely overlap, suggesting that the choice of orientation angle has a minimal impact on the hysteresis loop of the randomly oriented BST80 polycrystal. A comparison of the hysteresis loops between the <001>-textured BST80 polycrystal and the randomly oriented BST80 polycrystal reveals that, under identical electric field strengths, the <001>-textured BST80 polycrystal demonstrates a higher polarization intensity, thereby providing a theoretical foundation for subsequent calculations of ∆T.
Orientation angles associated with textured and non-textured ceramic samples
| Sample | Texture direction/NO | Angle of orientation |
| Sample 1 | <001> | (0°, 0°, 0°, 0°, 0°, 0°, 0°, 0°, 0°) |
| Sample 2 | NO | (-10°, -8°, -6°, -4°, 0°, 4°, 6°, 8°, 10°) |
| Sample 3 | NO | (-20°, -15°, -10°, -5°, 0°, 5°, 10°, 15°, 20°) |
| Sample 4 | NO | (-30°, -23°, -15°, -7°, 0°, 7°, 15°, 23°, 30°) |
| Sample 5 | NO | (-40°, -30°, -20°, -10°, 0°, 10°, 20°, 30°, 40°) |
| Sample 6 | NO | (-100°, -75°, -50°, -25°, 0°, 25°, 50°, 75°, 100°) |
| Sample 7 | NO | (-150°, -112°, -74°, -36°, 0°, 36°, 74°, 112°, 150°) |
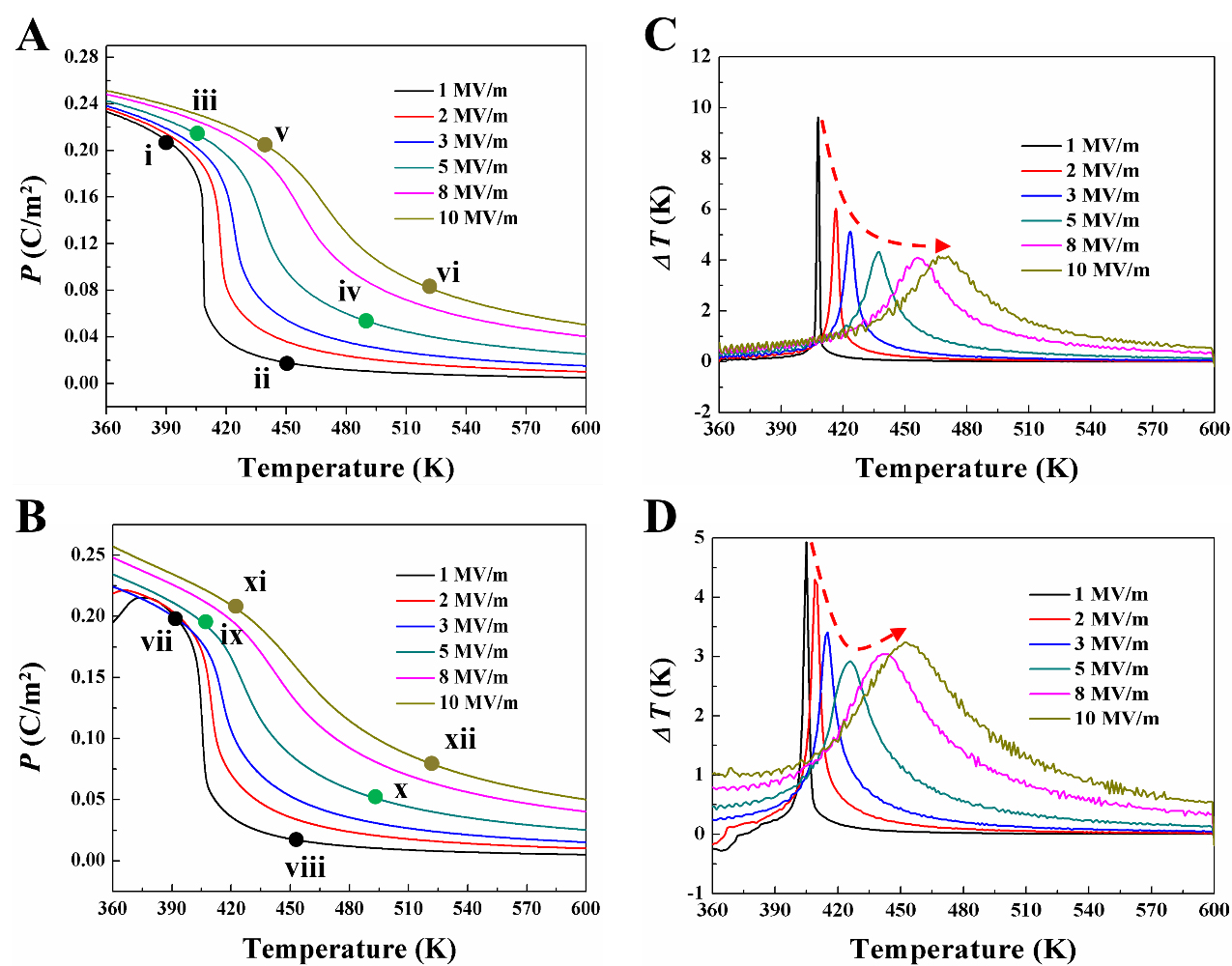
In calculating ∆T for both the <001>-textured BST80 polycrystalline and the randomly oriented BST80 polycrystalline, we employ the Maxwell relation. An electric field of 1 MV·m-1 is applied along the [001] direction to six groups of BST80 polycrystalline with varying random orientation angles. The relationship curve of ∆T versus temperature T is illustrated in Figure 4C, encompassing the six groups of random orientation angles. The resulting ∆T at corresponding temperatures of 350 K, 348 K, 347 K, 346 K, 346 K, and 347 K are 5.5 K, 4.5 K, 3.5 K, 4.5 K, 3.0 K, and 3.0 K, respectively. These data indicate that the orientation angle has a negligible effect on the ∆T of the randomly oriented BST80 polycrystalline. Consequently, we select the orientation angles of sample 5 for the BST80 polycrystalline to calculate ∆T under varying electric field strengths. According to the results presented in Figure 5A and 5B, we compute ∆T for this orientation of BST80 polycrystalline under electric field strengths of 1 MV·m-1, 2 MV·m-1, 3 MV·m-1, 5 MV·m-1, 8 MV·m-1, and 10 MV·m-1. The findings reveal that as the electric field strength increases, the ∆T for the BST80 polycrystalline with orientation angles of (-40°, -30°, -20°, -10°, 0°, 10°, 20°, 30°, 40°) at temperatures of 405 K, 410 K, 415 K, 425 K, 440 K, and 450 K are 4.9 K, 4.2 K, 3.4 K, 2.9 K, 3.1 K, and 3.2 K, respectively. The maximum ∆T exhibits a trend of initially decreasing, followed by an increase. Furthermore, the temperature range over which ∆T can be sustained gradually expands, suggesting that, from the perspective of phase transitions in ferroelectric materials, as the electric field strength increases, ferroelectric materials demonstrate characteristics indicative of a transition from first-order to second-order phase transitions. For the BST80 polycrystalline with a <001> texture, we apply electric field strengths of 1 MV·m-1, 2 MV·m-1, 3 MV·m-1, 5 MV·m-1, 8 MV·m-1, and 10 MV·m-1 to calculate ∆T. The P-T curve presented in Figure 5A and B demonstrates that as the electric field strength increases, the ferroelectric polarization value on the P-T curve progressively rises, indicating a transition from first-order to second-order phase transitions. In Figure 5C, the maximum ∆T values obtained at temperatures of 407 K, 418 K, 423 K, 437 K, 457 K, and 472 K are 9.6 K, 5.8 K, 5.2 K, 4.2 K, 4 K, and 4 K, respectively. Additionally, the temperature range over which ∆T can be sustained also gradually expands.
Figure 5. (A) The P-E loop curves of BST80 polycrystalline for sample 1, along with three sets of random orientation angles for samples 5, 6, and 7. The regions I-VI depicted in panel (B) illustrate the microscopic domain morphology at various phases of the P-E loop, encompassing scenarios both with and without the incorporation of textured ceramics, as shown in panel (A). The different colors observed within the ferroelectric domains represent the various types of domain structures, each characterized by distinct orientations. (C) The relationship curve between ΔT and temperature (T) generated by the BST80 polycrystalline under an electric field strength of 1 MV·m-1 for six sets of random orientation angles. BST80: Ba0.8Sr0.2TiO3; ΔT: temperature change.
By examining the ECE of both randomly oriented BST80 polycrystalline and the BST80 polycrystalline with a <001> texture, and comparing the enhancement effects of each, it is essential to analyze the relationship curves of ∆T and temperature between the two types of BST80 polycrystalline. As illustrated in Figure 5C and D under applied electric field strengths of 1 MV·m-1, 2 MV·m-1, 3 MV·m-1, 5 MV·m-1, 8 MV·m-1, and 10 MV·m-1, ∆T obtained from the BST80 polycrystalline with a <001> texture consistently exceeds that from the randomly oriented BST80 polycrystalline. This finding substantiates the efficacy of the <001>-textured BST80 polycrystalline in enhancing ECE under the influence of an electric field. Furthermore, a comparison of results across various electric field strengths reveals that the temperatures at which the BST80 polycrystalline with a <001> texture and the randomly oriented BST80 polycrystalline achieve their maximum ∆T are both shifted to higher values. Specifically, at electric field strengths of 1 MV·m-1, 2 MV·m-1, 3 MV·m-1, 5 MV·m-1, 8 MV·m-1, and 10 MV·m-1, the shifts are 2 K, 8 K, 8 K, 12 K, 17 K, and 22 K, respectively. The i-xii labels in Figure 5A and B, and Figure 6A and B indicate a one-to-one correspondence that illustrates the comparative analysis of the evolution of the polycrystalline ferroelectric domain structure before and after reaching the maximum ∆T under electric field conditions of 1 MV·m-1, 5 MV·m-1, and 10 MV·m-1, respectively. It is observed that both textured and random polycrystals exhibit higher polarization values when subjected to elevated electric fields compared to those exposed to lower electric fields, both before and after the phase transition induced by varying electric field strengths. This phenomenon is supported by the P-E loops presented in Figure 5 and the ferroelectric domain structures depicted in Figure 6. Furthermore, under high electric field conditions, the polarization at the grain boundaries aligns with the polarization direction within each grain, resulting in the formation of single domains.
Figure 6. The relationship between P, ΔT, and temperature T generated by the BST80 polycrystalline (A) and (C) represents sample 1 with <001>-oriented, while (B) and (D) depict sample 5 with random orientation angles under varying electric field strengths. ΔT: temperature change; BST80: Ba0.8Sr0.2TiO3.
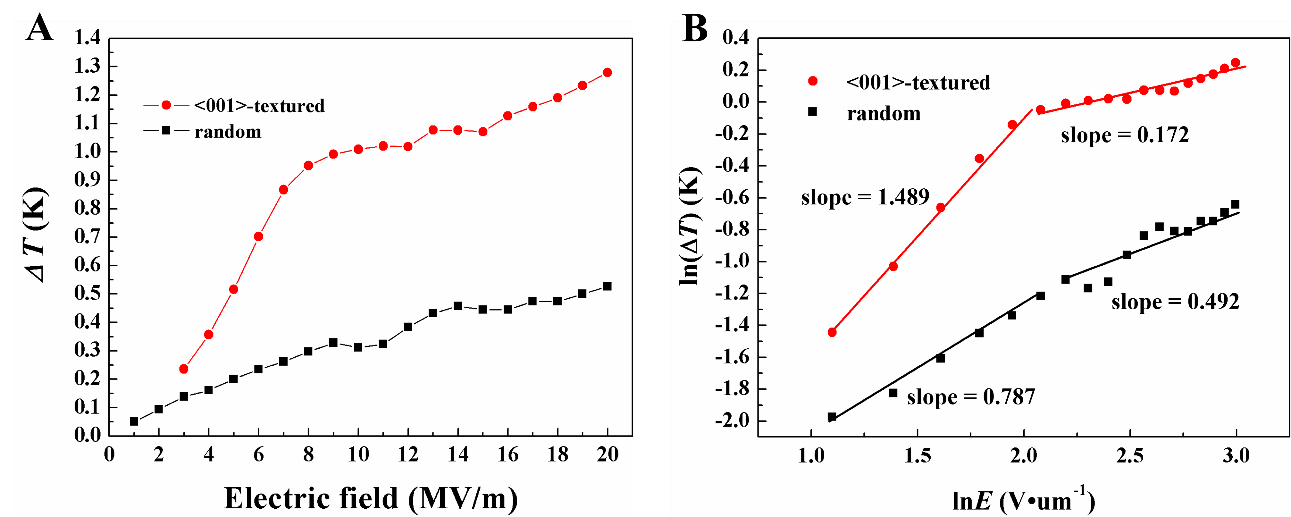
Figure 7A illustrates the electric field-induced ΔT of <001> oriented polycrystalline and randomly oriented polycrystalline materials subjected to varying electric fields at 360 K. The simulation results indicate that, for equivalent electric field strengths, the ΔT value for <001> oriented polycrystalline materials exceeds that of randomly oriented polycrystalline materials. This finding suggests that texturing significantly enhances the ECE in polycrystalline ceramics, which can be attributed to the increased polarization entropy associated with textured polycrystalline structures. To further elucidate the electrocaloric behavior, the simulation data have been reformulated using a logarithmic scale, as depicted in Figure 7B. Utilizing the theoretical framework established by Yan et al.[58], it is observed that in the low electric field regime, polarization varies almost linearly with the electric field, resulting in ΔT being proportional to the square of the spontaneous polarization. Consequently, ΔT exhibits a quadratic increase with the square of the electric field. Our findings indicate that the slope for <001> oriented polycrystalline materials in the low electric field range is 1.489, whereas the slope for randomly oriented polycrystalline materials is 0.787. This disparity may be attributed to the structural characteristics of the materials. In the high electric field regime, polarization behavior becomes nonlinear, influenced by various higher-order terms. As a result, textured polycrystalline structures and randomly oriented polycrystalline materials demonstrate distinct electrocaloric behaviors. Therefore, the phase-field simulation suggests that texturing treatments enhance the electrocaloric performance of polycrystalline ceramics, thereby providing a foundation for future experimental and theoretical investigations.
Figure 7. The sections labeled i-vi in panel (A) and vii-xii in panel (B) illustrate the microscopic domain morphology of the ceramic materials before and after achieving the maximum temperature difference (ΔT). This analysis encompasses both textured and non-textured materials, as shown in Figures 5(A) and 5(B), respectively, under different electric field conditions.
CONCLUSIONS
In this study, we employ the phase diagram of the solid solution BaxSr(1-x)TiO3, focusing on the relationship between Sr content and temperature, to identify the T phase of BST80 as our primary subject of investigation. We develop a polycrystalline model to examine the influence of the structural characteristics of ferroelectric polycrystalline ceramics, specifically comparing randomly oriented BST80 polycrystals with <001>-textured BST80 polycrystals, on their ECE performance. For the randomly oriented BST80 polycrystal, we select six distinct grain orientation angles for analysis. The results derived from the hysteresis loop calculations indicate that the BST80 polycrystal exhibiting orientation angles of (-40°, -30°, -20°, -10°, 0°, 10°, 20°, 30°, 40°) demonstrates optimal performance. Utilizing the Maxwell relation, we compute the adiabatic temperature change ∆T for both the randomly oriented and <001>-textured BST80 polycrystals under electric field strengths of 1 MV·m-1, 2 MV·m-1, 3 MV·m-1, 5 MV·m-1, 8 MV·m-1, and 10 MV·m-1. The findings reveal that the ∆T for the <001>-textured BST80 polycrystal exceeds that of the randomly oriented BST80 polycrystal. Additionally, the temperature at which the <001>-textured BST80 polycrystal achieves its maximum ∆T is observed to be shifted to a higher temperature compared to the randomly oriented BST80 polycrystal.
DECLARATIONS
Authors’ contributions
Conceived and designed the manuscript: Huang, H.; Shao, C.
Drafted and revised the manuscript: Huang, H.; Shao, C.
Availability of data and materials
Data that support the findings are available from the corresponding author upon reasonable request.
Financial support and sponsorship
This work was supported by the National Natural Science Foundation of China (Grant No. 92463306 and No. 52372100).
Conflicts of interest
Houbing Huang is Associate Editor of the journal Microstructures. Houbing Huang was not involved in any steps of editorial processing, notably including reviewer selection, manuscript handling, or decision making. Cancan Shao declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
2. Mensur-alkoy, E.; Okatan, M. B.; Aydin, E.; Kilic, Y.; Misirlioglu, I. B.; Alkoy, S. Effect of texture on the electrical and electrocaloric properties of 0.90Pb(Mg1/3Nb2/3)O3-0.10PbTiO3 relaxor ceramics. J. Appl. Phys. 2020, 128, 084102.
3. Cheng, L.; Ma, Z.; Lu, J.; Jiang, G.; Chen, K. Grain-orientation-engineered PMN-10PT ceramics for electrocaloric applications. J. Am. Ceram. Soc. 2023, 106, 1194-202.
4. Maurya, D.; Zhou, Y.; Yan, Y.; Priya, S. Synthesis mechanism of grain-oriented lead-free piezoelectric Na0.5Bi0.5TiO3-BaTiO3 ceramics with giant piezoelectric response. J. Mater. Chem. C. 2013, 1, 2102.
5. Zhang, H.; Xu, P.; Patterson, E.; Zang, J.; Jiang, S.; Rödel, J. Preparation and enhanced electrical properties of grain-oriented
6. Liu, K.; Ma, W.; Liu, F.; et al. Boosting electric-field-induced strain of dual templates-textured (Na1/2Bi1/2)TiO3-based lead-free piezoceramics by polarization coupling. J. Eur. Ceram. Soc. 2022, 42, 6466-77.
7. Bai, W.; Chen, D.; Zheng, P.; et al. Grain-orientated lead-free BNT-based piezoceramics with giant electrostrictive effect. Ceram. Int. 2017, 43, 3339-45.
8. Zhang, L.; Lin, J.; Li, G.; Qian, J.; Shen, B.; Zhai, J. Dual-template textured BNT-based ceramics with ultra-low electrostrain hysteresis. J. Eur. Ceram. Soc. 2024, 44, 7597-604.
9. Messing, G. L.; Trolier-mckinstry, S.; Sabolsky, E. M.; et al. Templated grain growth of textured piezoelectric ceramics. Crit. Rev. Solid. State. Mater. Sci. 2004, 29, 45-96.
10. Hiruma, Y.; Yoshii, K.; Nagata, H.; Takenaka, T. Phase transition temperature and electrical properties of
11. Cao, W.; Li, W.; Xu, D.; Hou, Y.; Wang, W.; Fei, W. Enhanced electrocaloric effect in lead-free NBT-based ceramics. Ceram. Int. 2014, 40, 9273-8.
12. Le, G. F.; Bennett, J.; Axelsson, A.; et al. Electrocaloric enhancement near the morphotropic phase boundary in lead-free NBT-KBT ceramics. Appl. Phys. Lett. 2015, 107, 172903.
13. Bai, W.; Xi, J.; Zhang, J.; Shen, B.; Zhai, J.; Yan, H. Effect of different templates on structure evolution and large strain response under a low electric field in <00l>-textured lead-free BNT-based piezoelectric ceramics. J. Eur. Ceram. Soc. 2015, 35, 2489-99.
14. Luo, L.; Dietze, M.; Solterbeck, C.; Es-souni, M.; Luo, H. Orientation and phase transition dependence of the electrocaloric effect in 0.71PbMg1/3Nb2/3O3-0.29PbTiO3 single crystal. Appl. Phys. Lett. 2012, 101, 062907.
15. Zhao, Y.; Gao, H.; Hao, X.; Zhang, Q. Orientation-dependent energy-storage performance and electrocaloric effect in PLZST antiferroelectric thick films. Mater. Res. Bull. 2016, 84, 177-84.
16. Hamad, M. A. Electrocaloric properties of Zr-modified Pb(Mg1/3Nb2/3)O3 polycrystalline ceramics. J. Adv. Dielect. 2013, 03, 1350029.
17. Hou, X.; Li, X.; Zhang, J.; Bag, S. P.; Li, H.; Wang, J. Effect of grain size on the electrocaloric properties of polycrystalline ferroelectrics. Phys. Rev. Appl. 2021, 15.
18. Su, Y.; Liu, N.; Weng, G. J. A phase field study of frequency dependence and grain-size effects in nanocrystalline ferroelectric polycrystals. Acta. Materialia. 2015, 87, 293-308.
19. Zhang, W.; Bhattacharya, K. A computational model of ferroelectric domains. Part II: grain boundaries and defect pinning. Acta. Materialia. 2005, 53, 199-209.
20. Hu, H.; Chen, L. Three-dimensional computer simulation of ferroelectric domain formation. J. Am. Ceram. Soc. 1998, 81, 492-500.
21. Ahluwalia, R.; Cao, W. Influence of dipolar defects on switching behavior in ferroelectrics. Phys. Rev. B. 2000, 63.
22. Wang, J.; Shi, S.; Chen, L.; Li, Y.; Zhang, T. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta. Materialia. 2004, 52, 749-64.
23. Li, Y.; Hu, S.; Liu, Z.; Chen, L. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films. Acta. Materialia. 2002, 50, 395-411.
24. Hwang, S. C.; Arlt, G. Switching in ferroelectric polycrystals. J. Appl. Phys. 2000, 87, 869-75.
25. Hwang, S. C.; Huber, J. E.; Mcmeeking, R. M.; Fleck, N. A. The simulation of switching in polycrystalline ferroelectric ceramics. J. Appl. Phys. 1998, 84, 1530-40.
26. Arlt, G. A model for switching and hysteresis in ferroelectric ceramics. Integr. Ferroelectr. 1997, 16, 229-36.
27. Kim, S. Polarization switching of ferroelectric ceramics with grain boundary effect: a simple continuum model. J. Appl. Phys. 2002, 92, 2668-73.
28. Rödel, J.; Kreher, W. S. Modelling linear and nonlinear behavior of polycrystalline ferroelectric ceramics. J. Eur. Ceram. Soc. 2003, 23, 2297-306.
29. Zhang, W.; Bhattacharya, K. A computational model of ferroelectric domains. Part I: model formulation and domain switching. Acta. Materialia. 2005, 53, 185-98.
30. Li, J. Y.; Rogan, R. C.; Ustündag, E.; Bhattacharya, K. Domain switching in polycrystalline ferroelectric ceramics. Nat. Mater. 2005, 4, 776-81.
31. Choudhury, S.; Li, Y.; Krilliii, C.; Chen, L. Phase-field simulation of polarization switching and domain evolution in ferroelectric polycrystals. Acta. Materialia. 2005, 53, 5313-21.
32. Choudhury, S.; Li, Y.; Krill, I. C.; Chen, L. Effect of grain orientation and grain size on ferroelectric domain switching and evolution: phase field simulations. Acta. Materialia. 2007, 55, 1415-26.
33. Huang, S.; Ma, C.; Jin, K. Advanced ferroelectric oxide films and heterostructures for unconventional applications. Adv. Phys:. X. 2025, 10, 2438686.
34. Wang, J. J.; Wang, B.; Chen, L. Q. Understanding, Predicting, and designing ferroelectric domain structures and switching guided by the phase-field method phase-field models for microstructure evolution. Ann. Rev. Mater. Res. 2019, 49, 127-152.
35. Gu, Y.; Meng, A. C.; Ross, A.; Chen, L. A phenomenological thermodynamic energy density function for ferroelectric wurtzite
36. Guo, C.; Huang, H. Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations. Microstructures 2022, 2, 21.
37. Hou, Y.; Li, J.; Yin, R.; et al. The critical role of phase transition and composition regulation in inorganic perovskite electrocaloric materials. J. Mater. Chem. C. 2025, 13, 5406-23.
38. Feng, H.; Hao, M.; Wu, G.; et al. Large electrocaloric effect and wide working area in the transition from ferroelectric to nanodomains. J. Am. Ceram. Soc. 2024, 107, 4777-88.
39. Ou, Y.; Lei, C.; Shan, D. Electrocaloric effect in different oriented BaZr0.15Ti0.85O3 single crystals. Materials. (Basel). 2022, 15, 7018.
40. Ullah, S.; Pramanik, T.; Kong, J.; Zheng, G. P.; Li, K.; Pramanik, A. Highly enhanced electrothermal properties of 001-textured Pb-free ferroelectric (Ba,Ca) (Ti, Zr, Sn)O3 for energy harvesting and solid-state cooling. J. Eur. Ceram. Soc. 2025, 45, 16830.
41. Lu, B.; Jian, X.; Lin, X.; et al. Enhanced electrocaloric effect in 0.73Pb(Mg1/3Nb2/3)O3-0.27PbTiO3 single crystals via direct measurement. Crystals 2020, 10, 451.
42. Jin, M.; Qiu, J.; Chen, Z.; Wang, X.; Yuan, N.; Ding, J. Electrocaloric effect of (110) oriented KNbO3 film. J. Nanosci. Nanotechnol. 2021, 21, 5247-52.
43. He, N.; Li, Q.; Lei, C.; et al. Electrocaloric response modulated by misfit strain in different oriented epitaxial ferroelectric thin films. Int. J. Solids. Struct. 2022, 252, 111808.
44. Lou, X. H.; Chen, Y. J.; Hou, X.; Wang, J.; Tian, X. B. Effects of the grain orientation on the electrocaloric effect of polycrystalline ferroelectrics. In 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, Proceedings of 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, IEEE Publishers: Piscataway, New Jersey, USA, 2022; pp 503-7.
45. Ünal, M. A.; Karakaya, M.; Irmak, T.; et al. Electrocaloric behaviour of tape cast and grain oriented NBT-KBT ceramics. J. Eur. Ceram. Soc. 2024, 44, 2128-34.
46. Shao, C.; Huang, H. Understanding thermal hysteresis of ferroelectric phase transitions in BaTiO3 with combined first-principle-based approach and phase-field model. Chinese. Phys. B. 2025, 34, 027701.
47. Zhang, J.; Hou, X.; Zhang, Y.; Tang, G.; Wang, J. Electrocaloric effect in ferroelectric materials: from phase field to first-principles based effective Hamiltonian modeling. Mater. Rep:. Energy. 2021, 1, 100050.
48. Chen, X.; Li, S.; Jian, X.; et al. Maxwell relation, giant (negative) electrocaloric effect, and polarization hysteresis. Appl. Phys. Lett. 2021, 118, 122904.
49. Nouchokgwe, Y.; Lheritier, P.; Hong, C. H.; et al. Giant electrocaloric materials energy efficiency in highly ordered lead scandium tantalate. Nat. Commun. 2021, 12, 3298.
50. Liu, X.; Wu, Z.; Guan, T.; et al. Giant room temperature electrocaloric effect in a layered hybrid perovskite ferroelectric:
51. Hadouch, Y.; Ben, M. S.; Mezzourh, H.; et al. Electrocaloric effect and high energy storage efficiency in lead-free
52. Shu, W.; Li, H.; Huang, Y.; et al. Frequency-dependent ferroelectric and electrocaloric properties in barium titanate-based ceramics based on Maxwell relations. J. Adv. Dielect. 2024, 14, 2440008.
53. Liu, Y.; Chen, X.; Han, Z.; Zhou, H.; Wang, Q. Defects in poly(vinylidene fluoride)-based ferroelectric polymers from a molecular perspective. Appl. Phys. Rev. 2022, 9, 031306.
54. Zheng, S.; Du, F.; Zheng, L.; et al. Colossal electrocaloric effect in an interface-augmented ferroelectric polymer. Science 2023, 382, 1020-6.
55. Yu, Y.; Du, H.; Yang, Z.; Li, J.; Qu, S. Electrocaloric effect of lead-free bulk ceramics: current status and challenges. J. Inorg. Mater. 2019, 35, 633-46. (in Chinese).
56. Liao, L.; Shan, D.; Lei, C.; Pan, K.; Li, J.; Liu, Y. Revealing the mechanisms of electrocaloric effects by simultaneously direct measuring local electrocaloric and electrostrain under ambient conditions. Acta. Materialia. 2024, 278, 120264.
57. Huang, Y. H.; Wang, J. J.; Yang, T. N.; Wu, Y. J.; Chen, X. M.; Chen, L. Q. A thermodynamic potential, energy storage performances, and electrocaloric effects of Ba1-xSrxTiO3 single crystals. Appl. Phys. Lett. 2018, 112, 102901.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Issue
Copyright
Data & Comments
Data






















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].